
























































МЕТОДИКА СТАТИСТИЧНОГО ТЕСТУВАННЯ
NIST STSТА МАТЕМАТИЧНЕ
ОБҐРУНТУВАННЯ ТЕСТІВ
Технічний звіт ІІТ – 001-2004 |
|
|
Заступник головного конструктора ____________________Потій О.В. “15” січня 2004 р. |
Виконавці Потій О.В. Лєншин А.В. Ізбенко Ю.А. |
2004
Зміст
Вступ. 3
1. Загальні положення. 4
2. Методика тестування. 7
3. Опис статистичних тестів. 8
4. Математичне обґрунтування тестів. 23
Висновки. 60
Література. 61
Вступ
Однією з складових оцінки стійкості криптографічних примітивів є оцінка статистичної безпеки даного примітиву. Вважається, що примітив є статистично безпечним, якщо послідовність, яку він генерує, за своїми властивостями не поступається випадковій послідовності; такі послідовності називаються "псевдо випадковими". Для оцінки того, наскільки близько примітиви апроксимують генератори "випадкових" послідовностей, використовуються статистичні тести. Запропонований NIST (Американським Національним Інститутом Стандартів) пакет тестів NIST STS для тестування генераторів випадкових або псевдо випадкових чисел є однім з підходів реалізації задачі оцінки статистичної безпеки криптографічних примітивів. Використання даного пакету дозволяє з високою долею ймовірності робити висновки щодо того, наскільки послідовність, що генерується досліджуваним примітивом, є статистично безпечною.
1. Загальні положення.
Набір тестів NIST STS був запропонований у ході проведення конкурсу на новий національний стандарт США блокового шифрування. Цей набір використався для досліджень статистичних властивостей кандидатів на новий блоковий шифр. На сьогодні методика тестування, що запропонована NIST є найбільш поширеною у розробників криптографічних засобів захисту інформації.
Порядок тестування окремої двійкової послідовності S має наступний вигляд [1]:
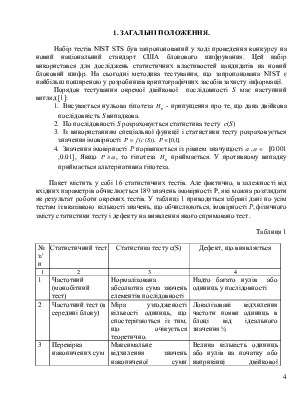
1.
Висувається нульова гіпотеза ![]() - припущення про те, що дана двійкова
послідовність S випадкова.
- припущення про те, що дана двійкова
послідовність S випадкова.
2. По послідовності S розраховується статистика тесту с(S)
3.
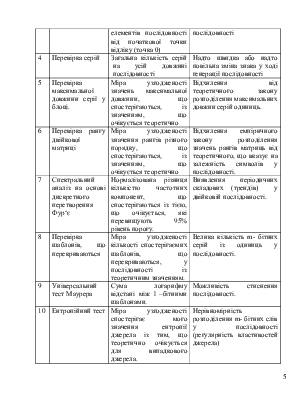
Із використанням спеціальної функції і статистики
тесту розраховується значення імовірності ![]()
4.
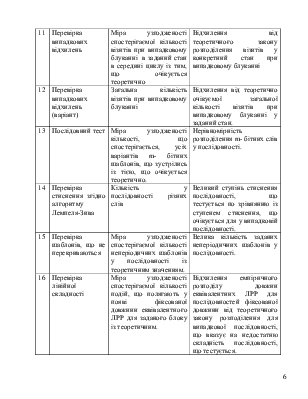
Значення імовірності Р порівнюється із
рівнем значущості ![]() ,
,![]()
![]() [0.001 ,0.01], Якщо
[0.001 ,0.01], Якщо ![]() , то гіпотеза
, то гіпотеза ![]() приймається.
У противному випадку приймається альтернативна гіпотеза.
приймається.
У противному випадку приймається альтернативна гіпотеза.
Пакет містить у собі 16 статистичних тестів. Але фактично, в залежності від вхідних параметрів обчислюється 189 значень імовірності Р, які можна розглядати як результат роботи окремих тестів. У таблиці 1 приводяться зібрані дані по усім тестам із вказівкою кількості значень, що обчислюються, імовірності Р, фізичного змісту статистики тесту і дефекту на виявлення якого спрямовано тест.
Таблиця 1
|
№ з/п |
Статистичний тест |
Статистика тесту c(S) |
Дефект, що виявляється |
|
1 |
2 |
3 |
4 |
|
1 |
Частотний (монобітний тест) |
Нормалізована абсолютна сума значень елементів послідовності |
Надто багато нулів або одиниць у послідовності |
|
2 |
Частотний тест (в середині блоку) |
Міра узгодженості кількості одиниць, що спостерігаються із тим, що очікується теоретично. |
Локалізовані відхилення частоти появи одиниць в блоці від ідеального значення ½ |
|
3 |
Перевірка накопичених сум |
Максимальне відхилення значень накопиченої суми елементів послідовності від початкової точки відліку (точка 0) |
Велика кількість одиниць або нулів на початку або наприкінці двійкової послідовності |
|
4 |
Перевірка серій |
Загальна кількість серій на усій довжині послідовності |
Надто швидка або надто повільна зміна знака у ході генерації послідовності |
|
5 |
Перевірка максимальної довжини серії у блоці. |
Міра узгодженості значень максимальної довжини, що спостерігаються, із значенням, що очікується теоретично |
Відхилення від теоретичного закону розподілення максимальних довжин серій одиниць. |
|
6 |
Перевірка рангу двійкової матриці |
Міра узгодженості значення рангів різного порядку, що спостерігаються, із значенням, що очікується теоретично |
Відхилення емпіричного закону розподілення значень рангів матриць від теоретичного, що вказує на залежність символів у послідовності. |
|
7 |
Спектральний аналіз на основі дискретного перетворення Фур‘є |
Нормалізована різниця кількістю частотних компонент, що спостерігаються із тією, що очікується, які перевищують 95% рівень порогу. |
Виявлення періодичних складових (трендів) у двійковій послідовності. |
|
8 |
Перевірка шаблонів, що перекриваються |
Міра узгодженості кількості спостерігаємих шаблонів, що перекриваються, у послідовності із теоретичним значенням. |
Велика кількість m- бітних серій із одиниць у послідовності. |
|
9 |
Універсальний тест Маурера |
Сума логарифму відстані між l –бітними шаблонами. |
Можливість стиснення послідовності. |
|
10 |
Ентропійний тест |
Міра узгодженості спостерігає мого значення ентропії джерела із тим, що теоретично очікується для випадкового джерела. |
Нерівномірність розподілення m- бітних слів у послідовності (регулярність властивостей джерела) |
|
11 |
Перевірка випадкових відхилень |
Міра узгодженості спостерігаємої кількості візитів при випадковому блуканні в заданий стан в середині циклу із тим, що очікується теоретично |
Відхилення від теоретичного закону розподілення візитів у конкретний стан при випадковому блуканні |
|
12 |
Перевірка випадкових відхилень (варіант) |
Загальна кількість візитів при випадковому блуканні |
Відхилення від теоретично очікуємої загальної кількості візитів при випадковому блуканні у заданий стан. |
|
13 |
Послідовний тест |
Міра узгодженості кількості, що спостерігається, усіх варіантів m- бітних шаблонів, що зустрілись із тією, що очікується теоретично. |
Нерівномірність розподілення m- бітних слів у послідовності. |
|
14 |
Перевірка стиснення згідно алгоритму Лемпеля-Зива |
Кількість у послідовності різних слів |
Великий ступінь стиснення послідовності, що тестується по зрівнянню із ступенем стиснення, що очікується для у випадковій послідовності. |
|
15 |
Перевірка шаблонів, що не перекриваються |
Міра узгодженості спостерігаємої кількості неперіодичних шаблонів у послідовності із теоретичним значенням. |
Велика кількість заданих неперіодичних шаблонів у послідовності. |
|
16 |
Перевірка лінійної складності |
Міра узгодженості спостерігаємої кількості подій, що полягають у появі фіксованої довжини еквівалентного ЛРР для заданого блоку із теоретичним. |
Відхилення емпіричного розподілу довжин еквівалентних ЛРР для послідовностей фіксованої довжини від теоретичного закону розподілення для випадкової послідовності, що вказує на недостатню складність послідовності, що тестується. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.