Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 19

Вищенаведені результати використовуються для тестування на випадковість у такий спосіб. Для “показового” набору х-значень (скажемо, 1 ≤ х ≤ 7 чи -7 ≤ х ≤ 1, -4 ≤ х ≤ 4  використовуються в даному пакеті) розраховуються частоти v_k(x) кількості k входжень у стан х під час J відхилень, що відбуваються в строці. Так,  з =1, якщо кількість входжень у х під час j-го відхилення (j = 1, …, J) точно дорівнює k, і =0 якщо навпаки. Поєднуються значення ξ(х) у класи, скажемо, k = 1, 2, …, 4 с додатковим класом  k ≥ 5. Теоретичні імовірності для цих класів:

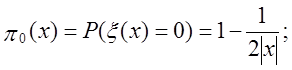
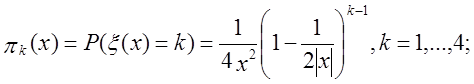
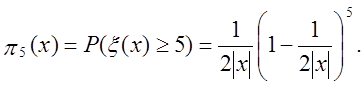
Дані імовірності мають вид

	π0(х)	π1(х)	π2(х)	π3(х)	π4(х)	π5(х)
х = 1	0,5000	0,2500	0,1250	0,0625	0,0312	0,0312
х = 2	0,7500	0,0625	0,0469	0,0352	0,0264	0,0791
х = 3	0,8333	0,0278	0,0231	0,0193	0,0161	0,0804
х = 4	0,8750	0,0156	0,0137	0,0120	0,0105	0,0733
х = 5	0,9000	0,0100	0,0090	0,0081	0,0073	0,0656
х = 6	0,9167	0,0069	0,0064	0,0058	0,0053	0,0588
х = 7	0,9286	0,0051	0,0047	0,0044	0,0041	0,0531

Дані частоти порівнюються з теоретичними за допомогою χ²-тесту

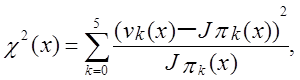
який для будь-якого х відповідно до гіпотези випадковості, повинний мати χ²-розподіл з 5 ступенями свободи. Це гарний тест, коли , тобто якщо . Якщо дана умова не задовольняється, величини ξ(х) повинні бути об'єднані у великі класи.

Відповідна множина Р-значень є звітною. Дані значення обчислюються відповідно до формули

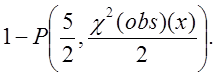
Приклад.

Вхід:

e = 0110110101.

Тест:

          Х = -1, 1, 1, -1, 1, 1, -1, 1, -1, 1,

          S₁ = -1,

          S₂ = -1 + 1 = 0,

S₃ = -1 + 1 + 1 = 1,

S₄ = -1 + 1 + 1 + (-1) = 0,

S₅ = -1 + 1 + 1 + (-1) + 1 = 1,

S₆ = -1 + 1 + 1 + (-1) + 1 + 1 = 2,

S₇ = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) = 1,

S₈ = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) + 1 = 2,

S₉ = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) = 1,

S₁₀ = -1 +1 + 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 = 2,

S = -1, 0, 1, 0, 1, 2, 1, 2, 1, 2,

          S^’ = 0, -1, 0, 1, 0, 1, 2, 1, 2, 1, 2, 0,

          J = 3: {0, -1, 0}, {0, 1, 0}, {0, 1, 2, 1, 2, 1, 2, 0}.

Стан х	Блок1{0,-1, 0}	Блок 2 {0,1,0}	Блок3 {0,1,2,1,2,1,2,0}
-4	0	0	0
-3	0	0	0
-2	0	0	0
-1	1	0	0
1	0	1	3
2	0	0	0
3	0	0	0
4	0	0	0

          v₀(-4) = 3,    v₁(-4) = v₂(-4) = v₃(-4) = v₄(-4) = v₅(-4) = 0,

          v₀(-3) = 3,    v₁(-3) = v₂(-3) = v₃(-3) = v₄(-3) = v₅(-3) = 0,

          v₀(-2) = 3,    v₁(-2) = v₂(-2) = v₃(-2) = v₄(-2) = v₅(-2) = 0,

          v₀(-1) = 2,    v₁(-1) = v₂(-1) = v₃(-1) = v₄(-1) = v₅(-1) = 0,

          v₀( 1) = 1,    v₁(1) = v₃(1) = 1, v₂(1) = v₄(1) = v₅(1) = 0,

          v₀( 2) = 2,    v₃(2) = 1, v₁(2) = v₂(2) = v₄(2) = v₅(2) = 0,

          v₀( 3) = 3,    v₁(3) = v₂(3) = v₃(3) = v₄(3) = v₅(3) = 0,

          v₀( 4) = 3,    v₁(4) = v₂(4) = v₃(4) = v₄(4) = v₅(4) = 0.

Для х = 1:

         

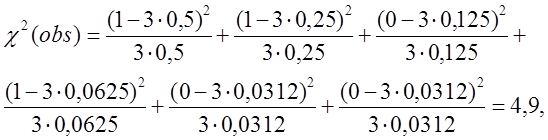
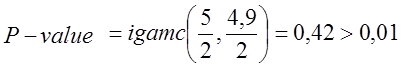           - для х = 1 тест пройдено.

4.16. Перевірка випадкових відхилень (варіант)

Альтернативою тесту випадкових відхилень може бути наступний. При використанні позначень попереднього тесту, нехай ξ_J(х) - загальна кількість входжень у х під час J відхилень (у стандартному коді тесту .). Оскільки S_k  обновляється кожним нулем, ξ_J(х) є сумою незалежних однаковим образом розподілених величин з однаковим розподілом ξ(х) = ξ₁(х). Отже, що обмежуючий розподіл ξ_J(х)

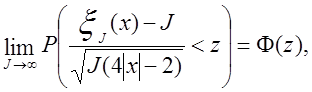
є нормальним. Гіпотеза випадковості може бути відхилена в тому випадку, коли Р-значення

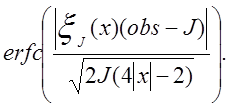
Приклад.