Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 9

класи	{v ≤ 10}		{v = 11}		{v = 12}		{v = 13}
імовірності	π0 = 0,0882		π1 = 0,2092		π2 = 0,2483		π3 = 0,1933
		{v = 14}		{v = 15}		{v ≥ 16}
		π4 = 0,1208		π5 = 0,0675		π6 = 0,0727

Велике значення χ² показує, що послідовність має скупчення одиниць; генерація «випадкових» послідовностей людиною має тенденцію до виникнення малих значень v_n [3].

Приклад.

Вхід: e =11001100000101010110110001001100111000

0000000010010011010101000100010011110101101000

00001101011111001100111001101101100010110010,

n=128,

М=8,

К = 3.

Тест:

e₁ = 11001100, максимальна довжина «блоку» = 2;

e₂ = 00010101, максимальна довжина «блоку» = 1;

e₃ = 01101100, максимальна довжина «блоку» = 2;

e₄ = 01001100, максимальна довжина «блоку» = 2;

e₅ = 11100000, максимальна довжина «блоку» = 3;

e₆ = 00000010, максимальна довжина «блоку» = 1;

e₇ = 01001101, максимальна довжина «блоку» = 2;

e₈ = 01010001, максимальна довжина «блоку» = 1;

e₉ = 00010011, максимальна довжина «блоку» = 2;

e₁₀ = 11010110, максимальна довжина «блоку» = 2;

e₁₁ = 10000000, максимальна довжина «блоку» = 1;

e₁₂ = 11010111, максимальна довжина «блоку» = 3;

e₁₃ = 11001100, максимальна довжина «блоку» = 2;

e₁₄ = 11100110, максимальна довжина «блоку» = 3;

e₁₅ = 11011000, максимальна довжина «блоку» = 2;

e₁₆ = 10110010, максимальна довжина «блоку» = 2;

v₀ = 4, v₁ = 9, v₂ = 3, v₄ = 0,

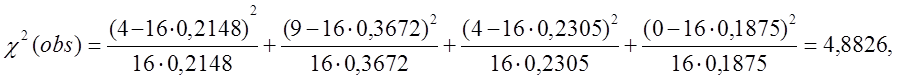
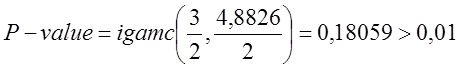 - тест пройдений.

4.5. Перевірка рангу двійкової матриці

Іншим підходом для тестування випадковості є розгляд лінійної залежності серед підстрок фіксованої довжини. Для цього будується матриця наступних друг за другом нулів і одиниць з послідовності, і перевіряється лінійна залежність серед рядків чи стовпців побудованої матриці.

Даний тест є різновидом одного з тестів, що входить у DIEHARD [4]. Він заснований на результатах, отриманих у [5] і [6]. Ранг R випадкової двійкової матриці M´Q приймає значення r = 0, 1, 2, …, m, де з імовірністю

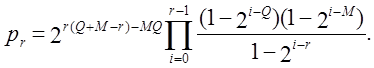
Значення імовірності фіксовані у стандартному коді пакета для M = Q = 32. Число М є параметром даного тесту, в ідеальному випадку n = M²N, де N є новим “розміром вибірки”. На практиці, значення для M і N вибираються таким чином, що відбракована частина рядка, n - M²N, була досить малою.

Логічним поясненням є те, що

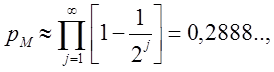
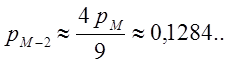
і всі інші імовірності є дуже малими (£ 0,005) коли М ³ 10.

Для матриці N обчислюються її ранги R_ℓ, ℓ = 1, …, N, і визначаються частоти F_M, F_M-1 і N  - F_M - F_M-1 величин М, М-1 і рангів, що не перевищують М – 2:

F_M = #{ R_ℓ = M},

F_{M - 1} = #{ R_ℓ = M - 1}.

Далі застосовується χ²  - тест із використанням класичної статистики

 ,

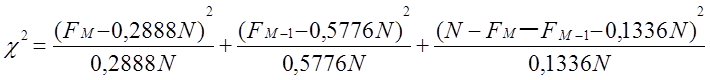що, відповідно до нульової гіпотези, має розподіл, близьке до χ² з 2 ступенями свободи. Р-значення має вид

exp{- χ²(obs)/2}.

Інтерпретація тесту така: велике значення χ²(obs) говорить про те, що відхилення рангу розподілу від відповідної випадкової послідовності є значним. Наприклад, псевдовипадкова матриця, яка генерується регістром зсуву, формується менш чим М послідовними систематичними векторами, що мають ранг R_ℓ ≡ М , у той час як для істинно випадкової послідовності такі події можуть наступити тільки з імовірністю 0,29.

Приклад.

Вхід: e = 01011001001010101101,

n = 20,

M = Q = 3.

Розбивка

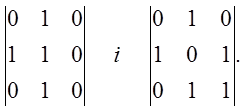
Визначимо ранг кожної матриці.

Нехай F_M – число матриць з рангом М,

           F_{M - 1}- число матриць з рангом М - 1,

           N - F_M - F_{M - 1} – число матриць, що залишилися.

Обчислимо статистику

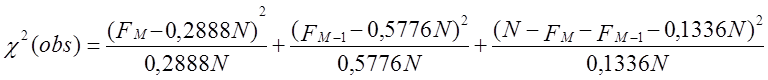
і значення P-value

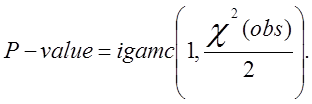
Значення P-value повинне бути більше 0,01.

Довжина послідовності, що рекомендується – не менш 38·M·Q біт.

4.6. Спектральний аналіз на основі дискретного перетворення Фур'є

Тест заснований на дискретному перетворенні Фур'є. Даний тест перевіряє періодичні тренди в серіях біт, що буде характеризувати відхилення від передбачуваної випадковості.