Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 6

Рекомендовані параметри тестування :

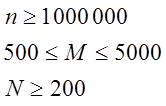                                                    (34)

3.12. Перевірка серій  (Serial Test)

Мета тесту – дослідити послідовність на випадковість  на основі аналізу довжин серій різної довжини.

Нехай  - двійкова послідовність довжини n та m - довжина серії Сформуємо послідовність , та додамо до кінця послідовності  перші m –1 бітів тієї ж самої послідовності. Підрахуємо кількість появ  усіх можливих серій, що пересікаються довжиною m, айві біти відкидаємо.  - довжиною m-1  та - довжиною m-1 .

Обчислимо статистики  [1]:

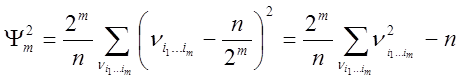 ,                        (35)

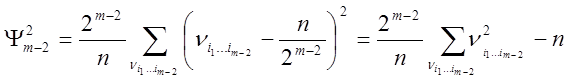,                   (36)

,                                                      (37)

                                         (38)

та значення   ,

,                                    (39)

                                    (40)

Значення  та  мають бути більше від 0.01.

Рекомендовані параметри тестування : .

3.13. Перевірка апроксимованої ентропії   (Approximate Entropy Test)

Мета тесту – дослідити послідовність на випадковість  на основі аналізу довжин серій різної довжини.

 Нехай  - двійкова послідовність довжини n та m - довжина серії Сформуємо послідовність , та додамо до кінця послідовності  перші m –1 бітів тієї ж самої послідовності. Роздивимося серії, що перетинаються довжиною m. Нехай  - кількість появ серій типу і.

Обчислимо  [1]

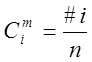,                                                         (41)

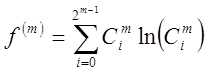.                                         (42)

(Порушуючи усі правила будемо вважати, що  )

Аналогічно поступимо із серіями, що перетинаються довжиною m+1.

Обчислимо статистику:

                        (43)

та значення

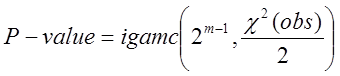.                     (44)

Значення  має бути більше від  0.01.

Рекомендовані параметри тестування:

3.14. Перевірка кумулятивних сум   (Cumulative sums (Casum) Test)

Мета тесту – дослідити послідовність на випадковість  на основі аналізу максимального відхилення суми елементів нормованої послідовності від нуля.

Нехай  - двійкова послідовність довжини n. Перетворимо її у послідовність Х:  (тобто 1®1, 0 ® -1).

Знайдемо максимальне відхилення суми

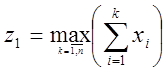 .                                             (45)

Обчислимо значення

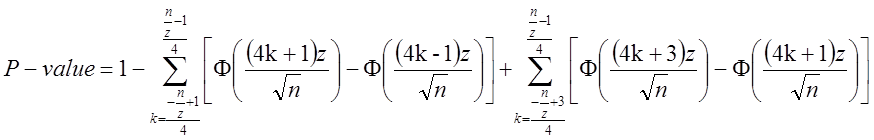
(46)

Аналогічні розрахунки проведемо для 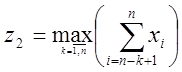  (рухаємося від кінця послідовності ). Незрозуміло, чому розробники не розглядають випадки 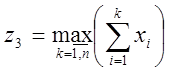 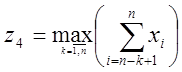    ; по значущості вони не поступаються  та   ( та   - визначають чи не переважають одиниці, а  та -  чи не переважають нулі).

Значення (,,  та  мають бути більше від 0.01

Рекомендована довжина послідовності: .

3.15. Перевірка випадкових відхилень-1  (Random Excursions Test)

Мета тесту – дослідити послідовність на випадковість  на основі аналізу  відхилення суми елементів нормованої послідовності від нуля.

Нехай  - двійкова послідовність довжини n. Перетворимо її у послідовність Х:  (тобто 1®1, 0 ® -1). Cформуємо послідовність:

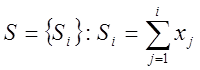.                                         (47)

Cформуємо послідовність:

                                           (48)

Розіб’ємо її на блоки, що мають вигляд , тобто на послідовності, у який перший та останній елементи дорівнюють нулю,  а всі інші відмінні від нуля.

Будемо вважати, що стан будь якого не нульового елементу х блоку може приймати одно із значень : (-4), (-3), (-2),...3, 4, тобто  .

Нехай  – кількість блоків у яких значення  х зустрічається рівно k разів,  . Кількість появ , що перевищують 5, будемо фіксувати у . Якщо, загальна кількість блоків дорівнює J , то .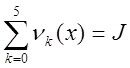

Обчислимо статистики для кожного х  [1]:

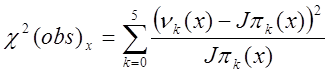.                                 (49)

Значення   беруться із таблиці 10.

Таблиця 10. Таблиця значень

x
± 1	0.5	0.25	0.125	0.0625	0.0312	0.0312
± 2	0.75	0.0625	0.0469	0.0352	0.0264	0.0791
± 3	0.8333	0.0278	0.0231	0.0193	0.0161	0.0804
± 4	0.8750	0.0156	0.0137	0.0120	0.0105	0.0733