Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 15

Існує кілька варіацій алгоритму Лемпеля-Зива. Тест, використовуваний у даному пакеті, оперує двійковою послідовністю  і діє в такий спосіб:

1.  Аналізує послідовність у послідовних непересічних строках (словах) таким чином, що наступне слово є найкоротшим рядком, що не зустрічалося раніше.

2.  Слова послідовно нумеруються по підставі 2.

3.  Кожному слову призначаються префікс і суфікс; префікс є числом попередніх слів, звірюваних з усіма, крім останнього розряду; суфікс є останнім розрядом.

Сила стиску – кількість аналізованих підстрок. Для малих n можливі випадки, коли стиск Лемпеля-Зива є більш довшим, ніж звичайне представлення.

Нехай W(n) означає кількість слів у розглянутій двійковій випадковій послідовності довжини n [10]. Тоді відомо, що

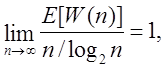
таким чином очікувана компресія є асимптотично добре апроксимиуємою , так що

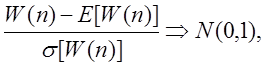
що має на увазі те, що центральна гранична теорема виконується для числа слів у стиску Лемпеля-Зіва.

Крім того, у [10] визначене значення .

У [11] доведено, що

 ,

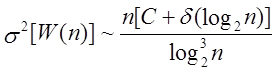де С = 0,26600 і  - безупинна функція із середнім значенням нуль, яка повільно варіює , і

У розглянутій послідовності рахується кількість слів. Виконання кодування Лемпеля-Зива необов'язкове, оскільки кількість слів, W, достатньо. W використовується для обчислення

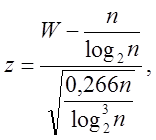
яке потім порівнюється зі стандартним нормальним розподілом.

P-значення обчислюється як

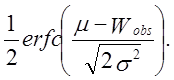
Для даного тесту середнє значення і дисперсія були розраховані з використанням SHA-1 для послідовності довжиною мільйон біт. Обчислені середнє значення і дисперсія рівні 69586,25 і 70,448718 відповідно.

Приклад.

Вхід: e = 010110010

Тест:

Позиція біту
1	Біт	Нове слово?	Слово
2	0	Так	0 (біт 1)
3	1	Так	1 (біт 1)
4	0	Ні
5	1	Так	01 (біти 3-4)
6	1	Ні
7	0	Так	10 (біти 5-6)
8	0	Ні
9	1	Ні

W_obs = 5(0, 1, 01, 10, 010).

4.11. Перевірка лінійної складності

Для перевірки випадковості тест використовує концепцію лінійної складності. Концепція лінійної складності пов'язана з популярною частиною багатьох генераторів ключового потоку, а саме лінійних рекурентних регістрів (ЛРР). Такі регістри довжини L складаються з L елементів, кожний з який має один вхід і один вихід. Якщо початковий стан ЛРР - (ε_L-1, …, ε₁, ε₀), то вихідна послідовність (ε_L, ε_L+1, …) задовольняє наступный рекурентній формулі для j ≥ L

Тут с₁, …, с_L – коефіцієнти утворюючого полінома відповідного ЛРР. Говорять, що ЛРР генерує дану двійкову послідовність, якщо дана послідовність є виходом ЛРР для деякого початкового стану.

Для заданої послідовності sⁿ = (ε₁, …, ε_n) її лінійна складність L(sⁿ) визначається як довжина самого короткого ЛРР, що генерує sⁿ з першими n символами. Можливість використання лінійної складності для тестування випадковості базується на алгоритмі Берлекемпа-Мессі, що забезпечує ефективну обробку кінцевих рядків.

Коли двійкова послідовність sⁿ дійсно випадкова, використовуються формули [12] для обчислення середнього значення µ_n = EL(sⁿ) і дисперсії  лінійної складності L(sⁿ) = L_n. Пакет Crypt-X говорить про те, що відношення  прагне до стандартної нормальної величини, так що Р-значення може бути знайдене з нормальної функції помилки. Разом з тим, стверджується [13], що “для великого n лінійна складність L(sⁿ) є приблизно нормально розподіленою із середнім n/2 і дисперсією 86/81, таким чином стандартна нормальна статистика 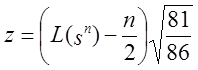”. Це зовсім неправильно. Навіть середнє значення µ_n не утримується асимптотично строго біля n/2, і при розгляді обмеженості дисперсії ця різниця стає значною. І, що ще більш важливо, імовірність великих відхилень обмежуючого розподілу є більшою, ніж той стандартний нормальний розподіл.