Після
цього переходимо до сканування тестового блоку. Перевіримо кожний із K блоків
і визначаємо відстань у блоках від останньої появи даного і-го блоку (тобто ![]() ), одночасно оновлюючи таблицю:
), одночасно оновлюючи таблицю: ![]() .
.
Обчислюємо статистику [1]
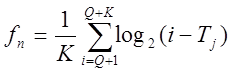 (25)
(25)
та
значення ![]()
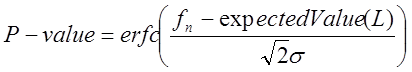 , (26)
, (26)
де 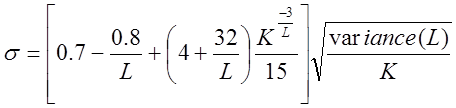 . (27)
. (27)
Значення expectedValue та variance беруться із таблиці 8.
Таблиця 8. Значення expectedValue та variance
|
l |
expectedValue |
variance |
|
1 |
0.7326495 |
0.690 |
|
2 |
1.5374383 |
1.338 |
|
3 |
2.4016068 |
1.901 |
|
4 |
3.3112247 |
2.358 |
|
5 |
4.2534266 |
2.705 |
|
6 |
5.2177052 |
2.954 |
|
7 |
6.1962507 |
3.125 |
|
8 |
7.1836656 |
3.238 |
|
9 |
8.1764248 |
3.311 |
|
10 |
9.1723243 |
3.356 |
|
11 |
10.170032 |
3.384 |
|
12 |
11.168765 |
3.401 |
|
13 |
12.168070 |
3.410 |
|
14 |
13.167693 |
3.416 |
|
15 |
14.167488 |
3.419 |
|
16 |
15.167379 |
3.412 |
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендовані параметри тестування подані у таблиці 9.
Таблиця 9. Рекомендовані параметри тестування
|
n |
L |
|
|
³ 387 840 |
6 |
640 |
|
³ 904 960 |
7 |
1 280 |
|
³ 2 068 480 |
8 |
2 560 |
|
³ 4 654 080 |
9 |
5 120 |
|
³ 11 342 400 |
10 |
10 240 |
|
³ 22 753 280 |
11 |
20 480 |
|
³ 49 643 520 |
12 |
40 960 |
|
³ 107 560 960 |
13 |
81 920 |
|
³ 231 669 760 |
14 |
163 840 |
|
³ 496 435 200 |
15 |
387 680 |
|
³ 1 059 061 760 |
16 |
655 360 |
3.10. Перевірка стиснення за допомогою алгоритму Лемпеля – Зева (Lempel-Ziv Compression Test)
Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу ступеня стиснення послідовності.
Нехай
![]() - двійкова послідовність довжини n.
Відокремимо від неї “слова”, що ідуть один за одним (послідовні ), але при
цьому не пересікаються і не повторюються, які утворюють “словник”.
- двійкова послідовність довжини n.
Відокремимо від неї “слова”, що ідуть один за одним (послідовні ), але при
цьому не пересікаються і не повторюються, які утворюють “словник”.
Підраховуємо
скільки слів у словнику ![]() та обчислюємо значення
та обчислюємо значення ![]() :
:
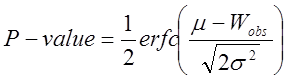 .
(28)
.
(28)
Для
вище приведеного прикладу ![]() .
.
У
дійсний час не існує теоретичних засобів для знаходження ![]() та
та ![]() . Для
даного тесту ці значення отримують, використовуючи генератор із функцією SHA-1
у ланцюгу зворотного зв’язку або генератор Blum – Blum – Shub.
. Для
даного тесту ці значення отримують, використовуючи генератор із функцією SHA-1
у ланцюгу зворотного зв’язку або генератор Blum – Blum – Shub.
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендована
довжина послідовності ![]() .
.
3.11. Перевірка лінійної складності (Linear Complexity Test)
Мета тесту – дослідити послідовність на випадковість на основі аналізу лінійної складності її послідовностей.
Нехай
![]() - двійкова послідовність довжини n.
Розіб’ємо її на
- двійкова послідовність довжини n.
Розіб’ємо її на 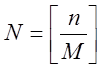 М-бітних підпослідовностей, що
не пересікаються. Зайві біти відкидаємо.
М-бітних підпослідовностей, що
не пересікаються. Зайві біти відкидаємо.
Визначимо
лінійну складність ![]() , кожної підпослідовності (тобто
мінімальну довжину ЛРР, яка необхідна для генерації даної підпослідовності).
Для обчислення лінійної складності можна використовувати алгоритм
Берлекампа-Мессі.
, кожної підпослідовності (тобто
мінімальну довжину ЛРР, яка необхідна для генерації даної підпослідовності).
Для обчислення лінійної складності можна використовувати алгоритм
Берлекампа-Мессі.
Находимо середнє значення:
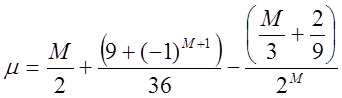 (29)
(29)
та обчислюємо статистику для кожної підпослідовності :
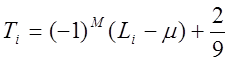 . (30)
. (30)
Значення Ti
розподіляється на К+1 категорій ![]() та обчислюється статистика:
та обчислюється статистика:
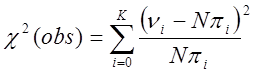 . (31)
. (31)
Розробники тесту не
вказали алгоритм розбиття. Значення ![]() визначається наступним
чином:
визначається наступним
чином:
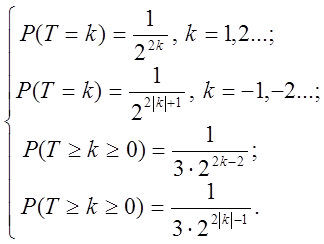 (32)
(32)
Обчилюємо
значення ![]()
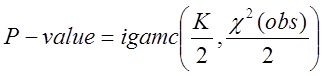 . (33)
. (33)
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.