Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 10

Нехай x_k – k-тий біт, де k = 1, …, n... Покладемо, що біти мають значення 1 і –1. Нехай

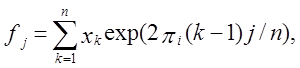
де exp(2πikj/n) = cos(2πkj/n) + i sin(2πkj/n), j = 0, …, n-1, і i ≡ . Через симетрію дійсного комплекснозначного перетворення розглядаються тільки значення від 0 до (n/2 - 1). Нехай mod_j – модуль комплексного числа f_j. При допущенні випадковості серій x_i, довірчий інтервал може бути обраний як значення з mod_j. Більш точно, 95% значень з mod_j повинні бути менше, ніж .

Р-значення, засноване на цій границі, має біноміальний розподіл. Нехай N₁ – кількість піків, менше чим h. Розглядаються тільки перші n/2 піків. Нехай N₀ = 0,95 N/2 і . Р-значення має вид

 ,

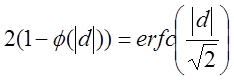де - інтегральна функція імовірності стандартного нормального розподілу.

Можливо й інше Р-значення, засноване на серіях f_j чи mod_j, що є чутливими до відхилення від випадковості. Однак, основне значення перетворення походить від графіка серій mod_j.

Відсутність даних про частотні компоненти

Наявність даних про частотні компоненти

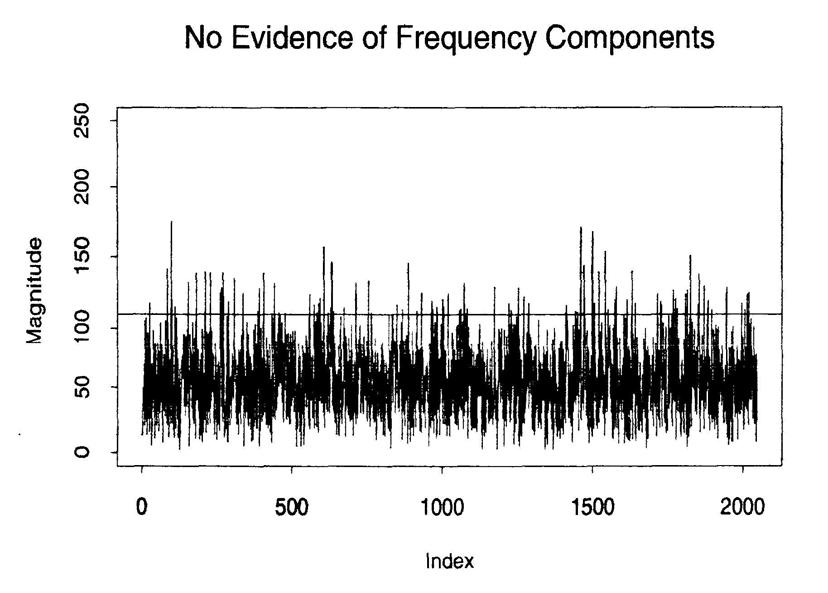
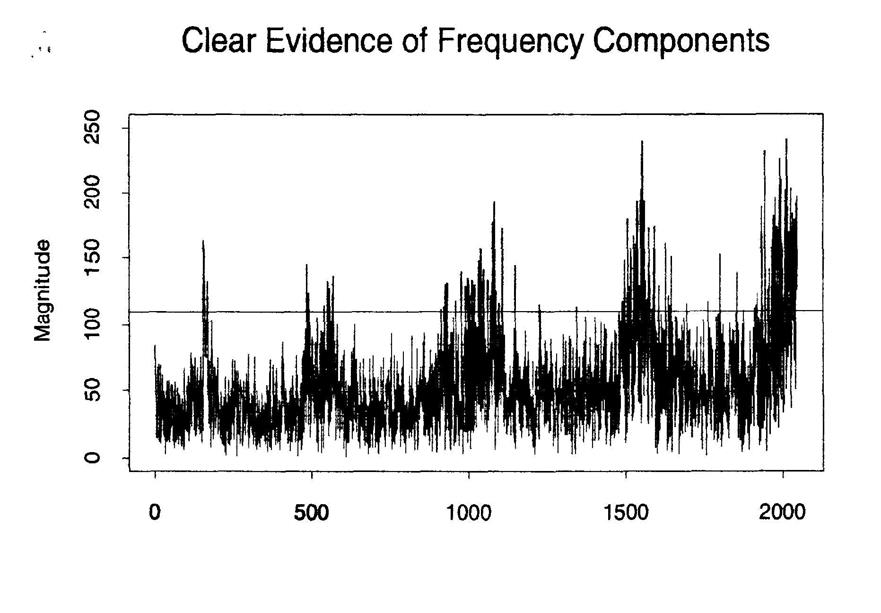
Рис.1. Результати тестування генераторів

На представленому рисунку верхній графік відображає серії з mod_j для 4096 біт, згенерованих гарним генератором. Лінія, що проходить через графік, позначає 95% довірчу границю. Р-значення для цих серій дорівнює 0,8077. Нижній графік відображає відповідний графік для генератора, що робить статистично пов'язані біти. На даному графіку значно більше, ніж 5% величин, лежать за межами довірчої границі. Р-значення для цих серій дорівнює 0,0001.

Приклад.

Вхід: e = 1001010011,

n=10.

Тест:

х = 1, -1, -1, 1, -1, 1, -1, -1, 1, 1,

S = DFT(x),

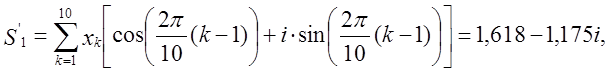
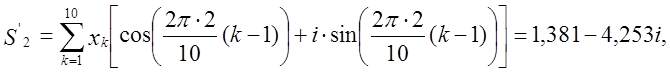
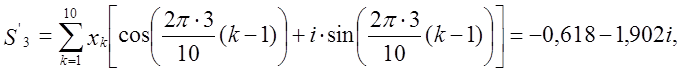
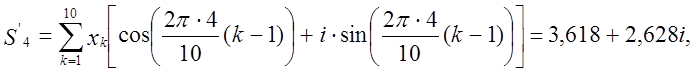
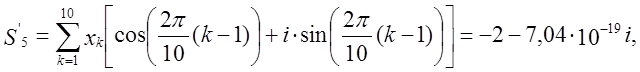
M₁ = modulus(1,618-1,175i) = 2,

M₂ = modulus(1,381-4,253i) = 4,472,

M₃ = modulus(-0,618-1,902i) = 2,

M₄ = modulus(3,618+2,628i) = 4,472,

M₅ = modulus(-2 - 7,04·10^-19 i) = 2,

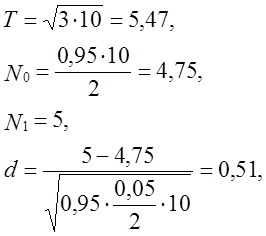
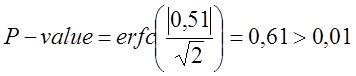- тест пройдено.

4.7. Перевірка шаблонів, що не перекриваються

Даний тест відбраковує послідовності, які занадто часто чи дуже рідко з'являються в даному аперіодичному шаблоні.

Нехай  - дане слово ( шаблон чи паттерн, тобто фіксована послідовність нулів і одиниць) довжини m. Даний шаблон вибирається як параметр тесту. Покладемо, тест заснований на шаблонах фіксованої довжини m. Нижче представлені таблиці обраних аперіодичних слів таких шаблонів для m = 2, …, 8...

Безліч періодів В

ß

відіграє важливу роль. Наприклад, коли В відповідає серії з m одиниць, ß = {1, …, m - 1}. Для вищезгаданого В ß=0, і В є аперіодичним шаблоном (тобто він не може бути записаний як СС…СС’ для шаблона З, що коротше чим В, де С’ позначає префікс С). У даній ситуації поява В в рядку є такою, що не перекривається.

У загальному випадку, нехай W = W(m, M) позначає кількість входжень даного шаблону В в строку. Помітимо, що статистика W визначена також для шаблонів В з ß ≠ 0. Найкращим шляхом обчислення W є обчислення W як суми

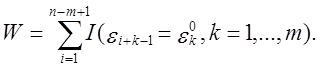
Випадкові величини  є m-залежними, таким чином Центральна Гранична Теорема здійсненна для W. Середнє і дисперсія апроксимуючого нормального розподілу мають вид

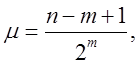
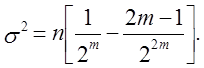
Для стандартних кодів програми M і N обрані таким чином, що n = MN і N = 8.

Вхідна строка розбивається на N блоків довжиною M. Нехай W_j = W_j (m, M) позначає кількість входжень шаблону В в блок j, j = 1, …, N.

Нехай µ = E W_j = (M – m + 1)2^-m. Тоді , для великих M, W_j виконується нормальний розподіл із середнім µ і дисперсією σ², і статистика

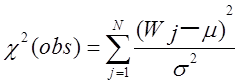
наближається до χ² – розподілу з N  ступенями свободи. Р-значення має вид .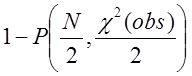

Тест може бути інтерпретований як відсікання послідовностей, що мають нерегулярне входження даного неперіодичного шаблона.

Таблиця 11. Неперіодичні шаблони для малих значень 2 ≤ m ≤ 5