Другие предметы \ Алгоритмические основы криптографии

Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 20

Вхід:

e = 0110110101.

Тест:

          Х = -1, 1, 1, -1, 1, 1, -1, 1, -1, 1,

          S1 = -1,

          S2 = -1 + 1 = 0,

S3 = -1 + 1 + 1 = 1,

S4 = -1 + 1 + 1 + (-1) = 0,

S5 = -1 + 1 + 1 + (-1) + 1 = 1,

S6 = -1 + 1 + 1 + (-1) + 1 + 1 = 2,

S7 = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) = 1,

S8 = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) + 1 = 2,

S9 = -1 + 1 + 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) = 1,

S10 = -1 +1 + 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 = 2,

S = -1, 0, 1, 0, 1, 2, 1, 2, 1, 2,

          S’ = 0, -1, 0, 1, 0, 1, 2, 1, 2, 1, 2, 0,

          J = 3: {0, -1, 0}, {0, 1, 0}, {0, 1, 2, 1, 2, 1, 2, 0},

          x(-1) = 1,

          x( 1) = 4,

          x( 2) = 3,

x(-9) = x(-8) = x(-7) = x(-6) = x(-5) = x(-4) = x(-3) = x(-2) = x(3) = x(4) = x(5) = x(6) = x(7) = x(8) = x(9) = 0.

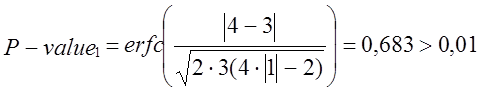 - для х = 1 тест пройдено.

Висновки

Завдяки значній кількості тестів, що використовуються, та гнучкості їх використання методика статистичного тестування NIST STS є досить гнучким та ефективним інструментом випробувань. Ефективність методики доведено досвідом її використання у національних конкурсах на розробку національних криптографічних стандартів. Методика NIST STS є одним з найкращих на цей час інструментів для проведення статистичних випробувань генераторів випадкових і псевдо випадкових послідовностей.

Література

1. A.Rukhin, J.Soto. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST Special Publication 800-22, 09.2000.

2. F. N. David and D. E. Barton, Combinatorial Chance. New York: Hafner Publishing Co., 1962, p. 230.

3. Pal Revesz, Random Walk in Random and Non-Random Environments. Singapore: World Scientic, 1990.

4. George Marsaglia, DIEHARD: a battery of tests of randomness. http://stat.fsu.edu/~geo/diehard.html.

5. I. N. Kovalenko (1972), Distribution of the linear rank of a random matrix, Theory of Probability and its Applications. 17, pp. 342-346.

6. G. Marsaglia and L. H. Tsay (1985), Matrices and the structure of random number sequences, Linear Algebra and its Applications. Vol. 67, pp.147-156.

7. O. Chrysaphinou and S. Papastavridis. A Limit Theorem on the Number of Overlapping Appearances of a Pattern in a Sequence of Independent Trials. Probability Theory and Related Fields, Vol. 79 (1988), pp. 129-143.

8. Ueli M. Maurer. A Universal Statistical Test for Random Bit Generators, Journal of Cryptology. Vol. 5, No. 2, 1992, pp. 89-105.

9. J. Ziv and A. Lempel (1977). A Universal Algorithm for Sequential Data Compression, IEEE Transactions on Information Theory. 23, pp. 337-343.

10. D. Aldous and P. Shields (1988). A Di_usion Limit for a Class of Randomly-Growing Binary Trees, Probability Theory and Related Fields. 79, pp. 509-542.

11. P. Kirschenhofer, H. Prodinger, and W. Szpankowski (1994). Digital Search Trees Again Revisited: The Internal Path Length Perspective, SIAM Journal on Computing. 23, pp. 598-616.

12. A. J. Menezes, P. C. van Oorschot, and S. A. Vanstone (1997). Handbook of Applied Cryptography. CRC Press, Boca Raton, FL.

13. H. Gustafson, E. Dawson, L. Nielsen, and W. Caelli (1994). A computer package for measuring the strength of encryption algorithms, Computers and Security. 13, pp. 687-697.

14. M. Kimberley (1987). Comparison of two statistical tests for keystream sequences," Electronics Letters. 23, pp. 365-366.

15. D. E. Knuth (1998). The Art of Computer Programming. Vol. 2, 3rd ed. Reading: Addison-Wesley, Inc., pp. 61-80.

16. S. Pincus and B. H. Singer. Randomness and degrees of irregularity, Proc. Natl. Acad. Sci. USA. Vol. 93, March 1996, pp. 2083-2088.

17. S. Pincus and R. E. Kalman. Not all (possibly) random sequences are created equal, Proc. Natl. Acad. Sci. USA. Vol. 94, April 1997, pp. 3513-3518.

18. A. Rukhin (2000). Approximate entropy for testing randomness, Journal of Applied Probability. Vol. 37, 2000.

19. Pal Revesz. Random Walk in Random And Non-Random Environments. Singapore: World Scientic, 1990.

20. Frank Spitzer. Principles of Random Walk. Princeton: Van Nostrand, 1964, (especially p. 269).

Скачать файл