![]() - кількість матриць, що
залишилось.
- кількість матриць, що
залишилось.
Обчислимо статистику [1]
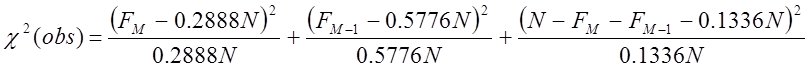 (13)
(13)
та
значення ![]()
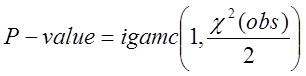 (14)
(14)
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендована
довжина послідовності – не менше від ![]() біт.
біт.
3.6. Спектральний тест (Discrete Fourier Transform (Spectral) Test )
Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу висоти викидів перетворення Фур’є .
Нехай ![]() - двійкова
послідовність довжини n. Перетворимо її у послідовність
- двійкова
послідовність довжини n. Перетворимо її у послідовність ![]() , де
, де ![]() (тобто
1→1, 0 → -1 ). Тепер застосуємо до х дискретне перетворення Фур’є та
отримаємо послідовність гармонік:
(тобто
1→1, 0 → -1 ). Тепер застосуємо до х дискретне перетворення Фур’є та
отримаємо послідовність гармонік:
S = DFT(x)/
Нехай S’ – підпослідовність S, що містить n/2
елементів S. Для кожного елементу ![]() знайдемо
модуль:
знайдемо
модуль: ![]() . (
. (![]() - є
комплексним числом). Підпослідовність М дасть нам послідовність висот
викидів перетворення Фур’є.
- є
комплексним числом). Підпослідовність М дасть нам послідовність висот
викидів перетворення Фур’є.
Знайдемо ![]() ,
, 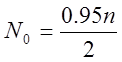 .
.
Обчислимо ![]() - кількість елементів М
менше від Т.
- кількість елементів М
менше від Т.
Обчислимо статистику [1]
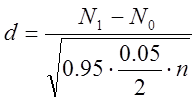 (15)
(15)
та
значення ![]()
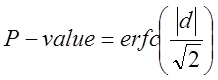 (16)
(16)
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендована довжина послідовності – не менше від 1000 біт
3.7. Перевірка шаблонів, що не перетинаються (Non-overlapping Template Matching Test)
Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу частоти зустрічі заздалегідь визначених шаблонів.
Нехай
![]() - двійкова послідовність довжини n.
Розіб’ємо її на
- двійкова послідовність довжини n.
Розіб’ємо її на 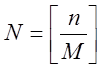 М-бітних
підпослідовностей. Зайві біти відкидаємо.
М-бітних
підпослідовностей. Зайві біти відкидаємо.
Нехай
![]() - кількість появ шаблону (підпослідовності
певного типу) в j-й підпослідовності (
- кількість появ шаблону (підпослідовності
певного типу) в j-й підпослідовності (![]() ). Пошук
здійснюється наступним чином. Нехай m- розмір шаблону у бітах. Починаємо
сканувати j-ю підпослідовність. Якщо набір, що розглядається
). Пошук
здійснюється наступним чином. Нехай m- розмір шаблону у бітах. Починаємо
сканувати j-ю підпослідовність. Якщо набір, що розглядається ![]() , співпадає із шаблоном, то значення
, співпадає із шаблоном, то значення ![]() збільшуємо на 1 та розглядаємо набір
збільшуємо на 1 та розглядаємо набір ![]() у противному випадку значення
у противному випадку значення ![]() не змінюємо та розглядаємо набір
не змінюємо та розглядаємо набір ![]() .
.
Сканування завершуємо, коли частина елементів набору виходить за границі послідовності. що роздивляється
Знаходимо
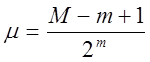 ,
(17)
,
(17)
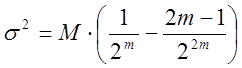 (18)
(18)
Обчислюємо статистику [1]
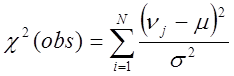 (19)
(19)
та значення ![]()
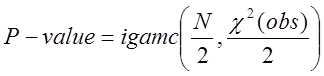 . (20)
. (20)
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендовані
параметри тестування : ![]() .
.
3.8. Перевірка шаблонів, що пересікаються (Overlapping Template Matching Test)
Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу частоти зустрічі заздалегідь визначених шаблонів.
Нехай
![]() - двійкова послідовність довжини n.
Розіб’ємо її на
- двійкова послідовність довжини n.
Розіб’ємо її на 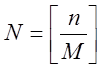 М-бітних підпослідовностей, що
не пересікаються. Зайві біти відкидаємо. Нехай
М-бітних підпослідовностей, що
не пересікаються. Зайві біти відкидаємо. Нехай ![]() -
кількість підпослідовностей, у яких шаблон з’являється і раз
-
кількість підпослідовностей, у яких шаблон з’являється і раз ![]() , де К – число ступенів свободи , в
, де К – число ступенів свободи , в ![]() записується кількість підпослідовностей, у
яких шаблон з’являється Л та більше разів. Пошук здійснюється наступним чином.
Нехай m - розмір шаблону у бітах. Починаємо сканувати j-ю підпослідовність,
записується кількість підпослідовностей, у
яких шаблон з’являється Л та більше разів. Пошук здійснюється наступним чином.
Нехай m - розмір шаблону у бітах. Починаємо сканувати j-ю підпослідовність,![]() . Розглядаємо набори, що пересікаються по m
біт.
. Розглядаємо набори, що пересікаються по m
біт.
Знаходимо
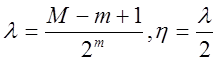 . (21)
. (21)
Обчислюємо статистику [1]
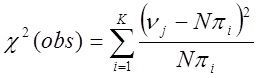 , (22)
, (22)
де
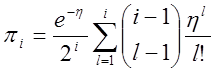 (23)
(23)
та
значення ![]()
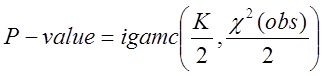 . (24)
. (24)
Значення
![]() має бути більше від 0.01.
має бути більше від 0.01.
Рекомендовані
параметри тестування : ![]() .
.
![]() .
.
3.9. Універсальний тест Маурера (Maurer’s “Universal Statistical” Test)
Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу відстаней між шаблонами.
Нехай
![]() - двійкова послідовність довжини n.
Розіб’ємо її на два сегмента: ініціалізуючий та тестовий. Перший складається із
Q блоків по L біт, другий -із К = [n/L] –Q
блоків по L біт. Зайві біти відкидаємо.
- двійкова послідовність довжини n.
Розіб’ємо її на два сегмента: ініціалізуючий та тестовий. Перший складається із
Q блоків по L біт, другий -із К = [n/L] –Q
блоків по L біт. Зайві біти відкидаємо.
Ініціалізуючий
сегмент використовується для створення таблиці. Для ![]() , де j
є десятирічне уявлення і-го L - річного блоку.
, де j
є десятирічне уявлення і-го L - річного блоку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.