Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 3

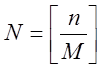Мета тесту – перевірити рівномірність появи 0 та 1 у підпослідовностях.  Нехай  - двійкова послідовність довжини n. Розіб’ємо її на  М-бітних підпослідовностей, які не пересікаються. Зайві біти відкидаємо. Визначимо долю одиниць у кожній підпослідовності [1]:

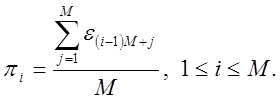                                    (6)

Обчислимо статистику

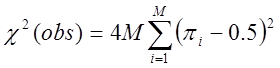                                     (7)

та значення

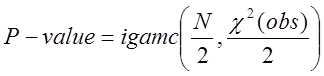.                                 (8)

Значення  має бути більше від  0,01. Рекомендована довжина послідовності – не менше від 100 біт.

3.3. Тест “дірок” (Runs Test).

Мета тесту – перевірити рівномірність розподілу 0 та 1 в послідовності, що досліджується на основі аналізу кількості появ “блоків” – підпослідовностей, що складаються із одних одиниць, та “дірок”- підпослідовностей, що містять лише нулі. Нехай  - двійкова послідовність довжини n.  Спочатку визначимо перед текстову статистику - долю одиниць у послідовності, що розглядається:

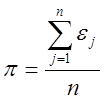.                                                     (9)

Якщо 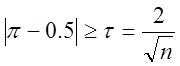, то тест вважається не пройденим. У противному випадку обчислимо статистику (кількість бітів та дірок):

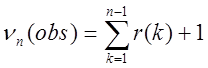,                                          (10)

де , якщо  та , якщо ,

та значення  [1]

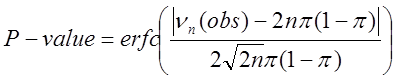                               (11)

Значення  має бути більше від  0.01.

Рекомендована довжина послідовності – не менше від 100 біт.

3.4. Тест “блоків” в підпослідовностях (Test for the Longest Run of Ones in a Block ).

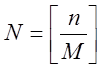Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу кількості появ “блоків” у підпослідовностях.  Нехай  - двійкова послідовність довжини n. Розіб’ємо її на  М-бітних підпослідовностей. Зайві біти відкидаємо.

Розподілимо кількість появ послідовностей із максимальною довжиною “блоку”, рівною l, по категоріям (таблиця 2)

Таблиця 2. Розподіл за категоріями в залежності від довжини  “блоку”.

Обчислимо статистику [1]:

.

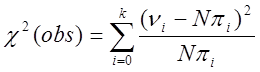Значення К визначаються по таблиці 3

Таблиця 3. Співвідношення між М та К

М	8	128
К	3	5	6

Значення беруться із таблиці 4

Таблиця 4. Значення   для різних М та

М=8
0.2148			0.3672				0.2305				0.1875
М=128
0.1174		0.2430			0.2493		0.1752		0.1027			0.1124
0.0882	0.2092			0.2483		0.1933		0.1208		0.0675			0.0727

Обчислимо значення

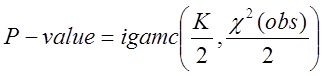                                       (12)

Значення  має бути більше від  0.01.

Рекомендована довжина послідовності – не менше від 100 біт. Значення М вибирається в відповідності до таблиці 5.

Таблиця 5. Співвідношення між М та мінімальною довжиною послідовності

min n	128	6272	750 000
M	8	128	104

3.5. Перевірка рангів матриці (Binary Matrix Rank Test)

Мета тесту – перевірити рівномірність розподілу 0 та 1 у послідовності, що досліджується на основі аналізу кількості появ матриць різних рангів.

Нехай  - двійкова послідовність довжини n. Розіб’ємо її на 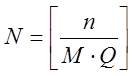 підпослідовностей які не пересікаються. Зайві біти відкидаємо. Тепер уявимо кожну таку підпослідовність як бінарну матрицю розміром M×Q.

Визначимо ранг матриці. Нехай

          - кількість матриць з рангом М,

        - кількість матриць з рангом М-1,