Другие предметы \ Алгоритмические основы криптографии

Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 8

c2 (obs) = 4×10×[(0,4 – 0,5)2 + (0,7 – 0,5)2 + (0,4 – 0,5)2 + (0,3 – 0,5)2 + (0,5 – 0,5)2 + (0,3 – 0,5)2 + (0,4 – 0,5)2 + (0,4 – 0,5)2 + (0,4 – 0,5)2 + (0,4 – 0,5)2] = 7,2,

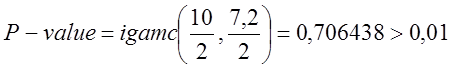 - тест пройдений.

4.3.Перевірка серій

Ціль тесту полягає в перевірці емпіричного і теоретичного значень кількості серій у рядку, що проходить тестування.

Даний тест заснований на розподілі загального числа серій, Vn. Для фіксованої пропорції  (яке відповідно до частотного тесту повинне бути визначене близько до 0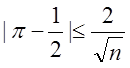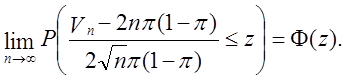,5: ).

                      (55)

Для обчислення Vn визначаються k = 1, …, n-1, r(k) = 0 якщо εk = εk+1 і r(k) = 0 якщо εk ≠ εk+1. Тоді  Р-значення визначається як

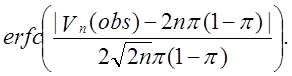
Приклад.

Вхід: e = 11001001000011111101101010100010001000010110100011

             00001000110100110001001100011001100010100010111000,

n=100.

Тест:

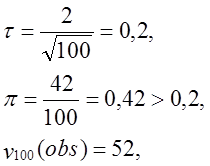
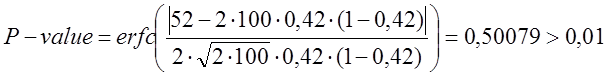 - тест пройдений.

4.4.Перевірка максимальної довжини серії у блоці

Довжина самої довгої серії з одиниць є іншою характеристикою, що може бути використана для тестування випадковості. Строка довжиною n, така що n = MN, повинна бути розбита на N підстрок, кожна довжиною M. Для тесту, заснованого на довжині самої довгої серії одиниць vj j-тої підстроки розміру М, обираються К+1 класів (у залежності від М). Для кожної з цих підстрок обчислюються частоти v0, v1, …, vК (v0 + v1 + … + vК = N, тобто обчислюються значення самої довгої серії одиниць усередині кожної з підстрок, що належать кожному з К+1 обраних класів). Якщо існує r одиниць і M-r нулів у m-бітному блоці, то умовна імовірність того, що самий довгий рядок одиниць v у цьому блоці менше або дорівнює m, має наступний вид з 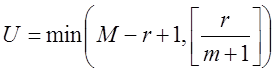 [2]:

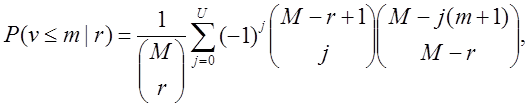
так що

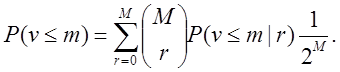                      (56)

Вираження (56) визначає теоретичні імовірності π0, π1, …, πДо даних класів.

Емпіричні частоти vj, i = 0, …, K, є матеріалом для обчислення χ2-статистики

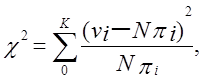
яка, відповідно до гіпотези випадковості, має наближений χ2-розподіл з К ступенями свободи. Р-значення обчислюється як

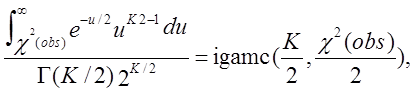
де Р(а, х) позначає гама функцію (див. частотний тест у блоці).

Представлена нижче таблиця містить обрані значення К і М з відповідними імовірностями, обчисленими відповідно до (56). Випадки з К = 3, М = 8; К = 5, М = 128; К = 6, М = 10000 використовуються в стандартному пакеті.

_____________________________________________________________

К = 3, М = 8

класи

{v ≤ 1}

{v = 2}

{v = 3}

{v ≥ 4}

імовірності

π0 = 0,2148

π1 = 0,3672

π2 = 0,2305

π3 = 0,1875

К = 5, М = 128

класи

{v ≤ 4}

{v = 5}

{v = 6}

{v = 7}

імовірності

π0 = 0,1174

π1 = 0,2430

π2 = 0,2493

π3 = 0,1752

{v = 8}

{v ≥ 9}

π4 = 0,1027

π5 = 0,1124

К = 5, М = 512

класи

{v ≤ 6}

{v = 7}

{v = 8}

{v = 9}

імовірності

π0 = 0,1170

π1 = 0,2460

π2 = 0,2523

π3 = 0,1755

{v = 10}

{v ≥ 11}

π4 = 0,1015

π5 = 0,1077

К = 5, М = 1000

класи

{v ≤ 7}

{v = 8}

{v = 9}

{v = 10}

імовірності

π0 = 0,1307

π1 = 0,2437

π2 = 0,2452

π3 = 0,1714

{v = 11}

{v ≥ 12}

π4 = 0,1002

π5 = 0,1088

К = 6, М = 10000

Скачать файл