Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 13

Приклад.

Вхід: e = 1010010010111001011010,

n = 22,

М = 10,m = 3,

шаблон дорівнює 001.

Тест:

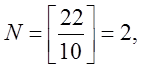
e₁ = 1010010010,

e₂ = 1110010110.

Позиції бітів	e1 = 1010010010		e2 = 1110010110
	Біти	v1	Біти	v2
1-3	101	0	111	0
2-4	010	0	110	0
3-5	100	0	100	0
4-6	001	1 (+1)	001	1 (+1)
5-7	Пропуск	1	Пропуск	1
6-8	Пропуск	1	Пропуск	1
7-9	001	2 (+1)	011	1
8-10	010	2	110	1

 

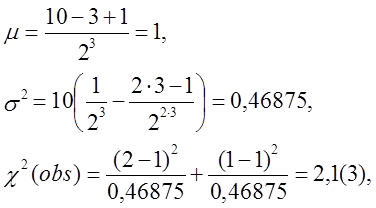
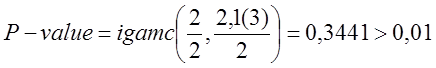 - тест пройдено.

4.8. Перевірка шаблонів, що перекриваються

Даний тест відтинає послідовності, що містять занадто багато чи занадто мало входжень m – серій, що містять одні одиниці, але можуть бути легко модифіковані перевіркою нерегулярних входжень будь-якого періодичного шаблону В.

Для виконання даного тесту вибираються M і N таким чином, що n = MN, тобто вхідна строка розбивається на N блоків, кожен довжиною M.

Нехай  позначає кількість (можливих перекриттів) серій одиниць довжини m у  j – му блоці. Асимптотичний розподіл  є складеним розподілом Пуассона [7]:

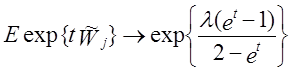                                       (57)

де (t є дійсним значенням).

Відповідні імовірності можуть бути виражені в термінах виродженої гіпергеометричної функції . Якщо U позначає випадкову величину зі складеним асимптотичним розподілом Пуассона , то для  з

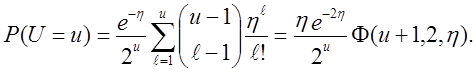
Наприклад,

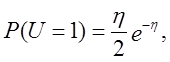
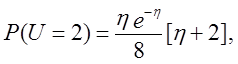
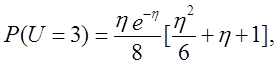
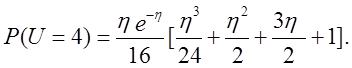
Доповнення до функції розподілу даної випадкової величини має вид

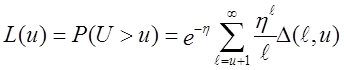
з

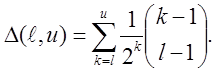
Вибираються К + 1 розрядів або чарунок для U, тобто {U = 0}, {U = 1}, …, {U = K - 1}, {U  ≥ K}. Теоретичні імовірності  цих чарунок обчислюються згідно представлених вище виражень. Раціональним вибором можуть бути

Після того, як U₁, …, U_N обчислено, знаходяться частоти v₀, v₁, …, v_До  кожної чарунки,  v₀ + v₁ + … + v_ДО = N, і розраховується значення статистики хі-квадрат

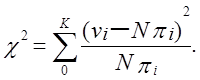
Вираження для визначення Р-значення використовуються ті ж самі, що й у тесті на шаблони, що не перекриваються. Інтерпретація результатів: для дуже малих значень досліджувана послідовність показує нерегулярні входження m-серій, що складаються з одиниць.

Приклад.

Вхід: e = 10111011110010110100011100101110111110000101101001101,

n = 53,

М = 10,

m = 2,

шаблон дорівнює 11,

К = 5.

Тест:

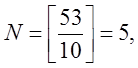
v₀ = 0, v₁ = 0, v₂ = 0, v₃ = 0, v₄ = 0, v₅ = 0.

e1 = 1011101111
Позиції бітів	Біти	Кількість появлень шаблону
1-2	10	0
2-3	01	0
3-4	11	1 (+1)
4-5	11	2 (+1)
5-6	10	2
6-7	01	2
7-8	11	3 (+1)
8-9	11	4 (+1)
9-10	11	5 (+1)
v0 = 0, v1 = 0, v2 = 0, v3 = 0, v4 = 0, v5 = 1.

Після тестування чотирьох послідовностей, що залишилися

v₀ = 0, v₁ = 2, v₂ = 0, v₃ = 1, v₄ = 1, v₅ = 1.

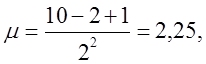
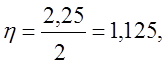
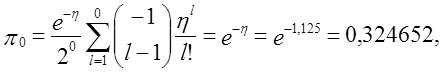
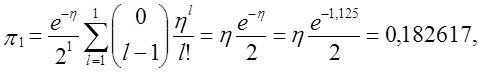
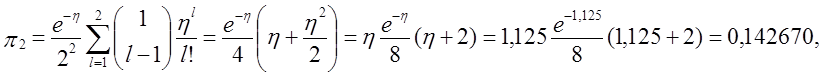
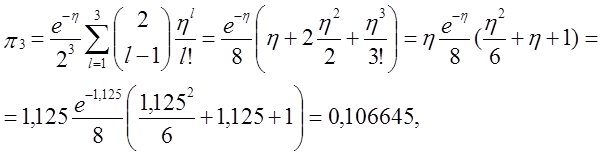
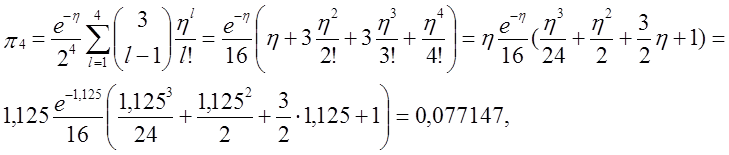
π₅ = 1 – π₀ – π₁ – π₂ – π₃ – π₄ = 1 - 0,324652 – 0,182617- 0,142670 – 0,106645 – 0,077147 = 0,166269,

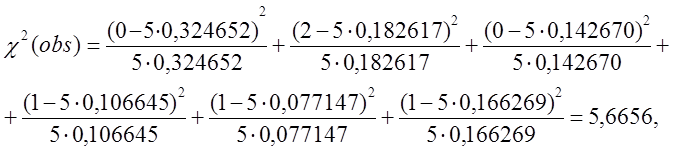
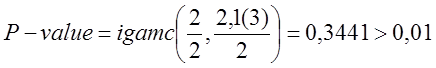 - тест пройдено.

4.9. Універсальний тест Маурера

Даний тест призначений не для перевірки дуже специфічних шаблонів чи типів статистичних дефектів. Проте тест сконструйований таким чином, «щоб бути здатним перевіряти один будь-який підклас із загального класу статистичних дефектів, що може бути змодельований ергодичним стаціонарним джерелом з кінцевою пам'яттю». Згідно твердження автора, тест відноситься до категорії стандартних статистичних тестів.