Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 18

              e' = 0100110101010,

              #0000 = 0, #0001 = 0, #0010 = 0, #0011 = 1, #0100 = 1, #0101 = 2, #0110 = 1, #0111 = 0,

              #1000 = 0, #1001 = 1, #1010 = 3, #1011 = 0, #1100 = 0, #1101 = 1, #1110 = 0, #1111 = 0;

            

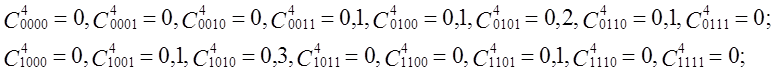
             j⁽⁴⁾ = 0×ln0 + 0×ln0 + 0×ln0 + 0,1×ln0,1 + 0,1×ln0,1 + 0,2×ln0,2 + 0,1×ln0,1 + 0×ln0 +

                         0×ln0 + 0,1×ln0,1 + 0,3×ln0,3 + 0×ln0 + 0×ln0 + 0,1×ln0,1 + 0×ln0 + 0×ln0 = -  1,8343;

c²(obs) = 2×10(ln2- j⁽³⁾ + j⁽⁴⁾) = 20×( ln2 + 1,6434 –1,8343) = 10,045,

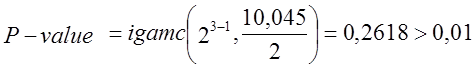 - тест пройдено.

4.14. Перевірка накопичених сум

Тест заснований на оцінці максимального абсолютного значення часткових сум послідовності, представленої у виді  Великі значення статистики показують, що існує занадто багато одиниць чи  занадто багато нулів у початкових фазах послідовності.  Малі значення показують, що нулі й одиниці перемішані занадто рівномірно. Двоїстий тест може бути отриманий з реверсированого випадкового блукання . Відповідно до даного визначення, інтерпретація результатів тесту модифікується заміною “початкових фазах” на “кінцевих фазах”.

Тест заснований на граничному розподілі максимальних абсолютних значень часткових сум, ,

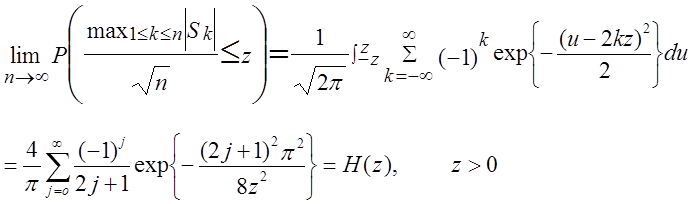            (62)

При статистиці тесту , гіпотеза випадковості є непридатною для великих значень z, і відповідне Р-значення має вид , де функція G(z) визначена формулою (63).

Серії H(z) в останньому рядку (62) сходяться швидко і повинні бути використані для чисельного обчислення тільки для малих значень z. Функція G(z) (яка еквівалентна H(z) для всіх z) краща для обчислення середніх і великих значень ,

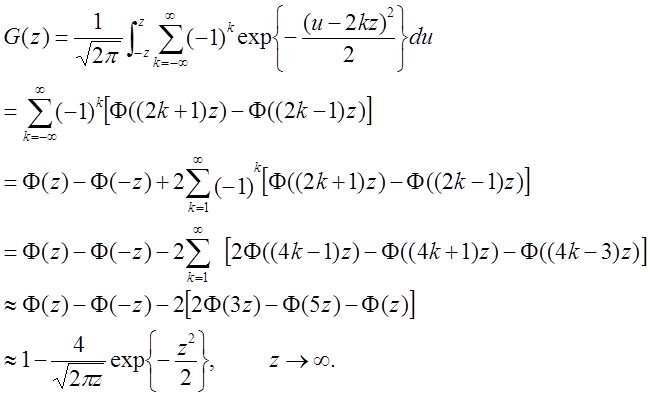                   (63)

де  - стандартний нормальний розподіл.

Більш точно, використовуючи Теорему 2.6, стор. 17 [19], обчислюють

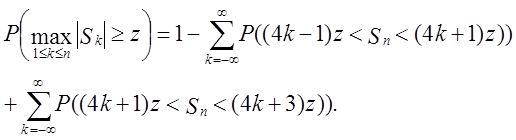
Формула використовується для обчислення Р-значення з

 .

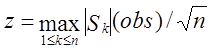Гіпотеза випадковості непридатна для великих значень z.

Приклад.

Вхід:

  e = 1011010111,

n = 10.

Тест:

  Х = 1, -1, 1, 1, -1, 1, -1, 1, 1, 1.

Прохід вперед:

S₁ = 1,

S₂ = 1 + (-1) = 0,

S₃ = 1 + (-1) + 1 = 1,

S₄ = 1 + (-1) + 1 + 1 = 2,

S₅ = 1 + (-1) + 1 + 1 + (-1) = 1,

S₆ = 1 + (-1) + 1 + 1 + (-1) + 1 = 2,

S₇ = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) = 1,

S₈ = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 = 2,

S₉ = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 + 1 = 3,

 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 + 1 + 1 = 4,

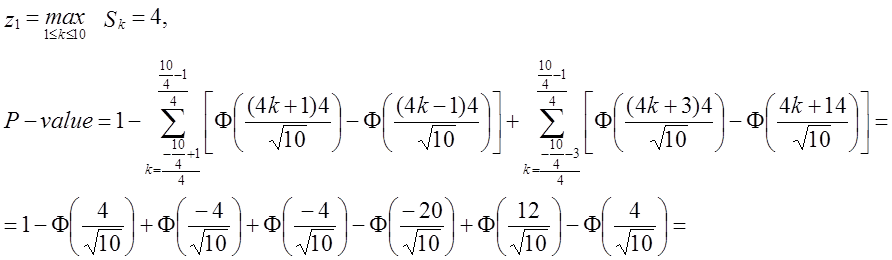
 - для проходу вперед тест пройдено.

4.15. Перевірка випадкових відхилень

Тест заснований на розгляді послідовних сум двійкових біт ( чи плюс мінус одиниць) як одно-розширене випадкове блукання. Тест перевіряє відхилення від розподілу числа появ випадкового блукання до визначеного “стану”, тобто будь-яке ціле значення.

Покладемо випадкове блукання S_k = X₁ + … X_k як послідовність відхилень до і від нуля

(i, …, ℓ) : S _{i - 1} =  S_{ℓ + 1} = 0,        S_k ≠ 0    для    i ≤ k ≤ ℓ.

Нехай J позначає загальну кількість таких відхилень у рядку. Обмежуюче розподіл для цього (випадкового) числа J (тобто числа нулів у сумі S_k, k = 1, 2, …, n, коли  S₀=0) має вид

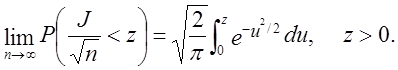                        (64)

Тест відхиляє гіпотезу випадковості, якщо J занадто мало, тобто якщо наступне Р-значення мале:

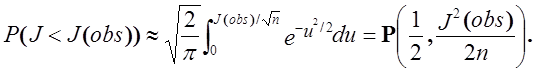
Якщо , гіпотеза випадковості відхиляється. У противному випадку розраховується число входжень випадкового блукання S у визначений стан.

Нехай ξ(х) – число входжень до х, х ≠ 0, під час 0-відхилення. Даний розподіл отриманий у [19], [20]:

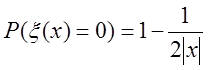                               (65)

і для k = 1, 2, …

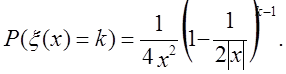                    (66)

Це позначає, що ξ(х) = 0 з імовірністю 1 – 1/2׀x׀; у противному випадку (з імовірністю 1/2׀x׀) ξ(х) збігається з геометричною випадковою величиною з параметром 1/2׀x׀.

Легко побачити, що

Еξ(х) = 1,

і

Var(ξ(х)) = .

Повна формула має вид:

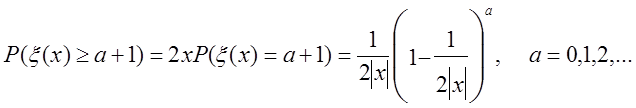          (67)