Разность потенциалов, как и разность значений потен-циальных энергий, от выбора точки отсчёта не зависит, а полностью определяется взаимным расположением интере-сующих нас точек в электрическом поле.
В механике показано, что в консервативных полях выполняется соотношение
F = -gradU.
Поскольку в электростатическом поле F = qE, а U = qj, то
qE = -grad qj = -q.gradj
или
.
В декартовых координатах это выражение имеет вид
.
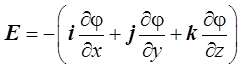Кстати, именно из этого выражения получена размерность напряженности [E] = В/м.
Знак «минус» в рассматриваемом выражении говорит о том, что вектор напряжённости всегда направлен в сторону максимально быстрого уменьшения потенциала.
Полученная связь между напряжённостью и потенциалом позволяет выявить ещё одну важную особенность электро-статического поля.
Если поле создано несколькими неподвижными зарядами, то напряжённость поля в любой точке равна векторной сумме напряжённостей, созданных каждым из зарядов в данной точке.
Следовательно, можно записать следующее соотношение:
j = j1 + j2 +...+ jn.
Таким образом, потенциал любой точки поля, созданного несколькими зарядами, равен алгебраической сумме потен-циалов, созданных каждым зарядом в данной точке.
Это означает, что потенциал, как и напряжённость, подчиняется принципу суперпозиции.
Электрическое поле
можно пред-ставить в графической форме. Для этого можно измерить или рассчитать
напряжённости электрического поля в различных точках и изобразить эти векторы
напряжённости. Полученное изображение будет содержать инфор-мацию о величине и
направлении напряжённости электрического поля в различных точках.
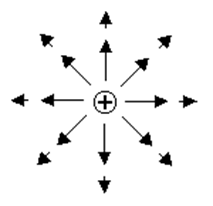
На рисунке показан пример изображения электрического поля точечного положительного заряда (рисунок выполнен без соблюдения масштаба).
Однако такой способ представления полей в графической форме не совсем удобен. Гораздо удобнее изображать элект-рическое поле с помощью силовых линий.
Силовая линия – это линия, касательная к которой в каждой точке совпадает по направлению с вектором напряжённости поля в этой точке.
Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. Соответственно силовые линии направлены от положительных зарядов к отрицательным.
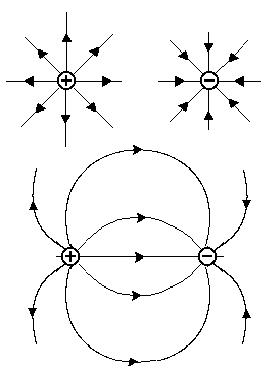Силовые линии принято
изображать так, чтобы их густота была больше там, где больше напряжённость
электростати-ческого поля.
Таким образом, если известна картина силовых линий электри-ческого поля, то можно судить о величине и направлении напря-жённости поля в различных точ-ках.
Важно отметить, что силовые линии не могут пересекаться. Это видно из следующего.
Направление напряжённости совпадает с направлением каса-тельной к силовой линии, прохо-дящей через эту точку.
Если силовая линия, проходя-щая через эту точку, пересекается другой силовой линией, то касательные к этим линиям имеют разные направления.
Поскольку напряжённость в любой точке имеет определённое направление, постольку невозможно и пересечение двух сило-вых линий.
Наряду с силовыми линиями для графического пред-ставления электростатических полей используют эквипотен-циальные поверхности, т. е. поверхности, все точки которых имеют одинаковый потенциал.
Пересечение эквипотенциальной поверхности с плоскостью листа даёт эквипотенциальную линию.
Если построить картину эквипотенциальных линий, в которой разность потенциалов между соседними эквипотенциалями оди-накова для всей картины, можно получить наглядное пред-ставление о электростатическом поле.
Знание картины эквипотенциальных линий позволяет по-строить и картину силовых линий. Это видно из следующего.
Если какой-либо заряд перемещается по эквипотенциальной поверхности, то работа электростатических сил равна нулю
A =-q(j2-j1) = 0,
так как на эквипотенциальной поверхности j1 = j2.
С другой стороны, работа кулоновских сил равна
,
и если заряд перемещается вдоль эквипотенциали, то она равна нулю:
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.