Курс общей физики для студентов ИДО. Часть II. Электростатика. Магнетизм. Колебания и волны: Учебное пособие, страница 3

F = F₁ + F₂ + F₃ +...+F_n .

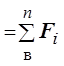Другими словами – результат взаимодействия заряда с несколькими другими зарядами является результатом наложения (суперпозиции) взаимодействий заряда q с каждым из зарядов
q₁, … q_n в отдельности.

Поэтому сила, действующая на заряд со стороны нескольких других зарядов, равна векторной сумме всех сил, действующих на интересующий нас заряд со стороны каждого из окружающих его зарядов в отдельности.

Это выражение представляет собой одну из возможных формулировок принципа суперпозиции.

Выражение для расчёта силы F можно записать в следующем виде:

= ,

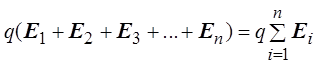где Е₁ – напряжённость поля, созданного зарядом q₁ в точке расположения заряда q, Е₂ – напряжённость поля, созданного там же вторым зарядом, Е_i – напряжённость поля, созданного i – м зарядом в точке расположения заряда q.

Сокращая q, получаем

.

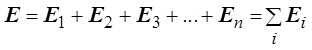Таким образом, напряжённость поля, созданного не-сколькими зарядами в интересующей нас точке, равна век-торной сумме напряжённостей, созданных каждым из заря-дов в этой точке.

Данное выражение представляет собой принцип супер-позиции для вектора напряжённости электрического поля.

В ряде случаев поле создаётся не точечными, а так называемыми распределёнными зарядами. Например, поле, соз-данное заряженной нитью.

В таких ситуациях распределённый заряд делят на малые порции dq_i, после чего рассчитывают напряжённость поля, используя принцип суперпозиции: 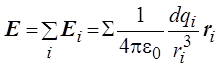, где r_i – вектор, соединяющий заряд dq_i c нужной точкой поля, r_i – модуль вектора r_i.

Учитывая, что dq_i является малой величиной, суммирование целесообразно заменить интегрированием

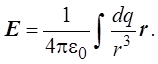
Величина dq может быть выражена следующим образом:

– если заряд распределён по линии, то dq = tdl, где t – линейная плотность заряда (это заряд единицы длины заряженной нити: );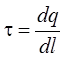

– если заряд распределён по поверхности, то dq = sds, где s – поверхностная плотность заряда (это заряд единицы площади заряженной поверхности: );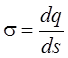

– если заряд распределён по объёму, то dq = rdV, где r – объёмная плотность заряда (это заряд единицы объёма заряженного тела: ).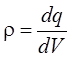

Важно отметить, что принцип суперпозиции полей справедлив для сред, свойства которых не зависят от величины напряжённости электрического поля. Например, в вакууме поле, созданное несколькими зарядами, равно сумме полей, созданных каждым из зарядов в отдельности. Для сегнетоэлектриков это утверждение неверно, так как их электрические свойства очень сильно зависят от напряжённости поля в сегнетоэлектрике.

Для большинства сред (газы, аморфные вещества, ряд кристаллических веществ) в слабых электрических полях прин-цип суперпозиции справедлив.

1.5. Поток вектора напряжённости

В ряде разделов курса общей физики рассматриваются векторные поля (например, электростатическое поле, магнитное поле).

В описании таких полей часто используют понятие потока вектора через некоторую поверхность. Рас-смотрим это понятие.

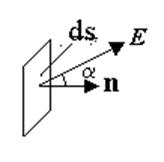
Пусть в некоторой области пространства существует электрическое поле. Выберем в этом поле элементарную площадку ds. Пусть нормаль к этой площадке n образует угол a c вектором напряжённости электрического поля (модуль вектора n = 1).

Потоком вектора напряжённости электрического поля через эту площадку называется величина, равная

,

где dФ – элементарный поток вектора напряжённости, Е – вектор напряжённости поля в пределах бесконечно малой площадки площадью ds.

Произведение En является скалярным, поэтому поток вектора напряжённости является скалярной величиной.

Иногда произведение nds заменяют на вектор ds, который направлен перпендикулярно плоскости площадки; модуль вектора ds равен площади элементарной площадки.

Поток напряжённости через конечную площадь s равен

.

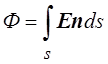В зависимости от величины угла между нормалью к площадке и вектором Е поток может быть положительным и отрицательным. Если угол между векторами Е и n острый, то поток положителен, если тупой – отрицателен.

Обратите внимание на то, что направление вектора n выбирается перед решением задачи произвольно (перпендикуляр к поверхности можно направить в две взаимно противоположные стороны). Поэтому знак потока вектора напряжённости опреде-ляется выбором направления вектора n.