Курс общей физики для студентов ИДО. Часть II. Электростатика. Магнетизм. Колебания и волны: Учебное пособие, страница 14

Как уже установлено, внутри заряженного проводника избыточные заряды и электрическое поле отсутствуют. Но это означает, что для равновесного распределения зарядов на поверхности проводника не имеет никакого значения наличие вещества внутри этого проводника, т. е. полость внутри провод-ника, во-первых, не повлияет на распределение зарядов на поверхности проводника, и, во-вторых, поля внутри этой полости не будет.

Отсюда следует, что в объёме, окружённом заряженной замкнутой проводящей оболочкой, поле всегда равно нулю.

Поле внутри полости равно нулю и тогда, когда оно создано не избыточным зарядом на поверхности полости, а внешним источником. В этом случае полость называют экраном, так как она может избавить от влияния электрических полей на тела (приборы), находящиеся внутри полости. Такие экраны широко применяются и в науке, и в технике.

Если внутрь незаряженной сферической полости радиуса r, поместить заряд q, картина изменится. Проведём анализ этой ситуации с помощью теоремы Гаусса.

В качестве поверхности интегрирования выберем сферу радиусом R < r, центр которой совпадает с центром полости.

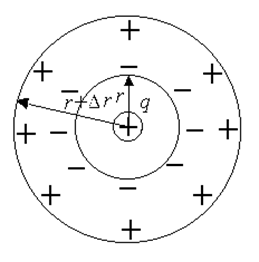Поток вектора напряжённости через эту поверхность не равен нулю, так как отличен от нуля заряд q, находящийся внутри полости. Другим словами – в этом случае поле внутри оболочки не равно нулю.

Внутри стенок проводящей обо-лочки электрическое поле должно быть равно нулю. Следовательно, поток вектора напряжённости через поверхность, проходящую внутри стенок проводящей оболочки
(r + dr > R > r), тоже должен быть равен нулю. Но это означает, что на внутренней поверхности оболочки должен быть распре-делён заряд, величина которого равна q, а знак противоположен знаку заряда, находящегося внутри полости.

В то же время, поскольку заряд оболочки, по условию, равен нулю, на внешней поверхности оболочки должен быть распре-делён заряд, величина и знак которого совпадают с зарядом q, находящимся внутри полости.

Вне оболочки (R > r + dr) поток вектора напряжённости не равен нулю, так как не равен нулю заряд внутри оболочки.

Таким образом, поле в этой ситуации существует внутри полости и вне оболочки. Если заряд, нахо-дящийся внутри оболочки точечный, то это поле точечного заряда.

Обратите внимание: если оболочку с находящимся внутри зарядом заземлить, то избыточный заряд с внешней поверхности оболочки сте-чёт, и поле вне оболочки станет равно нулю.

1.21.  Электроёмкость уединённого проводника

Как было показано в разд. 1.14, заряженный проводник эквипотенциален, а избыточный заряд определённым образом распределён по его поверхности.

Характер распределения заряда по поверхности проводника зависит от формы проводника*.

Если сообщить проводнику дополнительный заряд, то он распределится по его поверхности подобно первой порции заряда, поскольку форма проводника, по условию, не изменяется.

Но это означает, что при увеличении заряда уединённого проводника в n раз во столько же раз увеличится и напря-жённость поля, созданного проводником.

Это, в свою очередь, означает, что в n раз возрастёт и работа, необходимая для перемещения пробного заряда из бесконечности к проводнику, т. е. его (проводника) потенциал.

Следовательно, заряд проводника и его потенциал прямо пропорциональны друг другу.

Отношение заряда проводника к его потенциалу называется электроёмкостью (или просто ёмкостью) уединённого провод-ника:

.

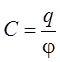Размерность электроёмкости [С] = Кл/В = Ф (фарада).

Следует заметить, что на практике используются меньшие величины единицы ёмкости. Это микрофарада (мкФ), равная
1^.10^-6Ф, и пикофарада (пФ), равная 1^.10^-12Ф  и др.

Важно отметить, что ёмкость проводника зависит от окружающих его тел.

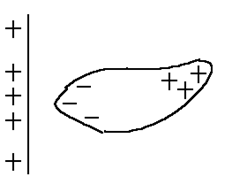Это объясняется тем, что окру-жающие тела значительно влияют на поле, созданное проводником, за счёт индуцированных в окружающих те-лах зарядов. Например, при прибли-жении к положительно заряженной плоскости другого проводника на нём происходит перераспределение заря-дов: на ближайшей к заряженной плоскости поверхности скапливают-ся отрицательные заряды, на удалённой – положительные. Эти заряды создают электрическое поле, которое в свою очередь влияет на распределение зарядов на плоскости.