__________________
* Если вокруг данного проводника имеются другие тела, то это повлияет на распределение заряда по поверхности проводника; но в данном случае рас-сматривается уединенный проводник.
Поскольку отрицательные заряды в данном случае распо-ложены к плоскости ближе, их влияние сильнее и потенциал плоскости понизится. Это означает, что ёмкость плоскости растёт.
Полученный вывод является общим: электрическая ёмкость проводника, окружённого другими проводниками, всегда больше ёмкости такого же уединённого проводника.
Если взять систему из двух проводников*, имеющих одинаковые по величине и противоположные по знаку заряды, то мы получим конденсатор – устройство, ёмкость которого намного больше ёмкости уединённого проводника и не зависит от ёмкости окружающих тел**.
Основной характеристикой
конденсатора является его ёмкость С, определяемая выражением 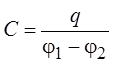 , где q – заряд обкладки
конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора.
, где q – заряд обкладки
конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора.
В данном случае разность
потенциалов между обкладками конденсатора равна напряжению на конденсаторе j1 – j2 =
U. Поэтому определение ёмкости конденсатора можно записать в таком виде:
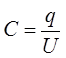 .
.
Ёмкость конденсатора зависит от площади обкладок конденсатора, формы обкладок, расстояния между ними, ди-электрической проницаемости вещества, заполняющего прост-ранство между обкладками конденсатора.
Рассмотрим в качестве примера плоский конденсатор. Это устройство из двух проводящих плоскостей, параллельных друг другу и разделённых слоем диэлектрика.
Если размеры пластин достаточно велики по сравнению с расстоянием d между ними, то заряд распределён по поверхности пластин равномерно с плотностью s = q/S.
_____________________
* Такие проводники принято называть обкладками.
** Емкость конденсатора не зависит от окружающих тел, поскольку практически все поле сосредоточено между его обкладками.
|
|
Одна пластина создаёт поле
напряжённостью 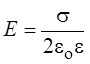 ; в соответствии с принципом
суперпозиции поле между пластинами
; в соответствии с принципом
суперпозиции поле между пластинами 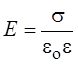 , вне пластин Е =
0.
, вне пластин Е =
0.
Поскольку 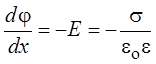 , то
, то
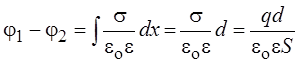 .
.
Отсюда ёмкость плоского конденсатора
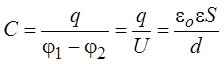 .
.
 В практической
деятельности часто используются соединения нескольких конденсаторов. Два
основных способа соединения конденсаторов – параллельное и последовательное.
Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых
конденсаторов.
В практической
деятельности часто используются соединения нескольких конденсаторов. Два
основных способа соединения конденсаторов – параллельное и последовательное.
Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых
конденсаторов.
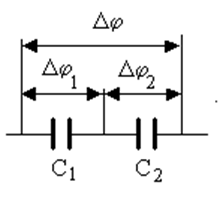
Последовательное соединение. По-следовательным называют соединение конденсаторов, показанное на рисунке.
|
Внутренние обкладки конденсаторов С1 и С2 заряда от батареи не получают. Но если левая обкладка С1 заряжена положительно, то на правую перетечёт такой же заряд противоположного знака с левой обкладки С2. Поэтому все обкладки конденсаторов будут иметь одинаковые по величине заряды q.
При таком соединении суммарная разность потенциалов на всех конденсаторах равна сумме разностей потенциалов на них Dj = Dj1 + Dj2.
Суммарную разность
потенциалов Dj можно выразить через заряд и суммарную
ёмкость конденсаторов C: 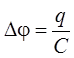 .
.
Разность потенциалов между
обкладками каждого из конденсаторов можно выразить аналогичным образом: 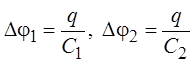 .
.
Заменяя разности потенциалов на приведённые выражения, получаем
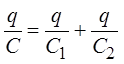
и, сокращая заряд, получаем выражение для суммарной ёмкости последовательно соединённых конденсаторов
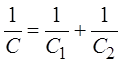 .
.
Таким образом, величина, обратная суммарной ёмкости конденсаторов, равна сумме обратных каждой из ёмкостей величин. Очевидно, что если соединены не два, а несколько конденсаторов, в сумме будет столько членов, сколько соединено конденсаторов.
Параллельное соединение. Параллельным называют показанное на
ри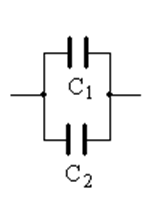 сунке соединение
конденсаторов.
сунке соединение
конденсаторов.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.