где n – единичный вектор, параллельный скорости направленного движения положительных зарядов; dS^ – площадь элементарной поверхности, перпендикулярной скорости направленного движе-ния зарядов.
Размерность плотности тока [j] = A/м2.
Сила тока и плотность тока связаны между собой:
.
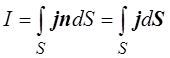Последнее выражение можно прочесть и так: сила тока через поверхность S равна потоку вектора плотности тока j через эту поверхность.
|
|
Протекание электрического тока не вызывает накопления заряда в проводнике. Это означает, что если в некоторый объём проводника вошёл заряд dq, то такой же заряд должен выйти из этого объёма.
В математической форме послед-нее утверждение имеет следующий вид:
.
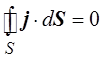Найдём связь плотности тока со средней скоростью упорядоченного движения зарядов в проводнике. Для этого выберем единичную поверхность, перпендикулярную скорости упорядоченного движения зарядов. За единицу времени через неё пройдёт n+×vположительных зарядов и n × v отри-цательных зарядов (здесь n+, n- – концентрации положительных и отрицательных зарядов соответственно, v+, v- – скорости направленного движения зарядов). Тогда плотность тока
j = e+ × n+ × v+ + e- × n- × v - .
В отсутствие электрического поля свободные носители заряда движутся хаотически. Это движение не даёт вклада в j, так как средняя скорость хаотического движения равна нулю.
Если в проводнике создать электрическое поле, свободные заряды начнут двигаться упорядоченно, т. е. возникнет электрический ток.
Однако этот ток очень быстро прекратится, так как свободные заряды перераспределятся так, что поле внутри проводника станет равно нулю и причина, вызвавшая направленное движение зарядов, исчезнет (см. разд. 1.19).
|
|
Для того чтобы ток не прекращался, необ-ходимо переносить из-быточные заряды с одного конца провод-ника на противополо-жный. Тогда электри-ческое поле внутри проводника будет су-ществовать непрерывно и направленное движение зарядов не будет прекращаться.
Другими словами – для того чтобы в цепи непрерывно существовал электрический ток, в части электрической цепи свободные носители должны двигаться по электрическому полю, а в другой части – против.
Естественно, электрическое поле не может заставить поло-жительные заряды двигаться против кулоновских сил. Следо-вательно, в части цепи должны действовать силы, заставляющие положительные заряды двигаться от “минуса” к “плюсу”. Такие силы неэлектростатического происхождения принято называть сторонними.
Участок цепи, на котором действуют сторонние силы, называют источником ЭДС (электродвижущей силы).
На практике используются различные виды источников ЭДС. Это электрические генераторы, гальванические элементы (батарейки), аккумуляторы и т. д.
Источник электродвижущей силы характеризуется величиной эдс:
,
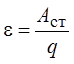где Аст – работа сторонних сил по перемещению заряда q; q – заряд, перемещённый сторонними силами.
Размерность ЭДС [e] = Дж/Кл = В (вольт).
Работу сторонних сил по перемещению заряда q внутри источника эдс можно вычислить следующим образом:
.
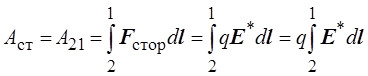Отсюда величина эдс
.
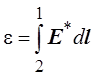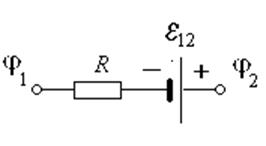Если электрическая
цепь замк-нута, то эдс равна
.
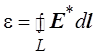Работа по перемещению заряда на участке цепи, содержащем источник ЭДС, может быть найдена как
.
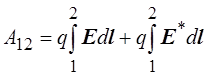Учитывая связь напряжённости и потенциала, а также опреде-ление ЭДС, получаем
.
Величина, равная работе электростатических и сторонних сил по перемещению единичного заряда в электрической цепи, называется напряжением:
.
Обратите внимание: напряжение на участке цепи и разность потенциалов на его концах различны по величине.
Напряжение и разность потенциалов не одно и то же!
Следует отметить, что участок цепи, содержащий источник ЭДС, называют неоднородным. Участок, не содержащий источ-ника ЭДС, называют однородным.
Поскольку однородный
участок не содержит ЭДС, постольку 
, т. е. напряжение на
однородном участке цепи равно разности потенциалов на его концах.
Георг Ом, экспериментируя с цепями постоянного тока, обнаружил, что сила тока в участке электрической цепи определяется следующим соотношением:
,
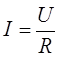Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
