Таким образом, получена
характеристика электрического поля, не зависящая от связанных зарядов.
Использование такой характеристики даёт очевидные преимущества. Действительно,
используя электрическое смещение, можно рассчитать электрическое поле (значение
вектора D) как внутри диэлектрика, так и вне его, учитывая только
свободные заряды. После этого легко найти напряжённость электрического поля в
любой точке,
______________________________
* В анизотропных диэлектриках диэлектрическая проницаемость является тензорной величиной и, в общем случае, D и Е по направлению не совпадают.
просто поделив значение D в этой точке на значение ди-электрической проницаемости e в этой точке и на электрическую постоянную eо.
Рассчитывать электрическое поле в пространстве с ди-электриком можно с помощью теоремы Гаусса. Применительно к электрическому смещению она в любой среде имеет вид
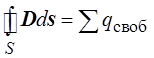
и может быть прочитана следующим образом: поток вектора электрического смещения через замкнутую поверхность ра-вен сумме свободных зарядов, охваченных этой поверх-ностью *. Знать, каковы по величине связанные заряды и как они распределены в пространстве, в этом случае не нужно.
Рассмотрим границу раздела двух изотропных диэлектриков с диэлектрическими проницаемостями e1 и e2 (e1 < e2).
Пусть на границе раздела свободные заряды отсутствуют.
Оба диэлектрика находятся в однородном электрическом поле напряжённостью Е. Напряжённость электрического поля в одном из диэлектриков будет равна Е1, во втором – Е2.
|
|
Выберем некоторый контур, охватывающий границу раздела двух сред.
Поскольку электрическое поле консервативно, работа куло-новских сил на замкнутом конту-ре Al равна нулю
Al = A12 + A23+ A34+ A41=0.
На участках 12 и 34 рассматриваемого контура работа
.
_____________________________
* В случае использования вектора напряженности теорема Гаусса имеет вид
В этих выражениях Е1t и Е2t – проекции векторов Е1 и Е2 на ось, параллельную границе раздела двух диэлектриков.
Пусть l23 = l41 ® 0. Тогда работа кулоновских сил на этих участках будет равна нулю.
Тогда работа кулоновских сил на всей длине контура
Al = A12 +A34 = 0
и
A12 = -A34.
Последнее соотношение можно переписать в виде
.
Сократив одинаковые множители, получаем
.
Таким образом, компонента вектора напряжённости, парал-лельная границе раздела двух сред (тангенциальная компонента), с обеих сторон от границы одинакова.
Вектор электрического смещения D = eoeE. Следовательно,
D1t = eoe1E1t,
D2t = eoe2E2t,
А это, в свою очередь, означает, что
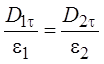
или
.
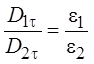Другими словами – тангенциальная компонента вектора (Dt) на границе раздела скачкообразно изменяется в соответствии с последним соотношением.
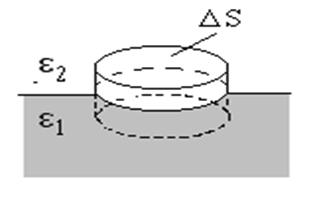Теперь рассмотрим поведение компонент векторов D
и E, перпендикулярных границе раз-дела двух диэлектриков. Для
этого воспользуемся теоремой Гаусса. В качестве поверхности интегрирования
выберем цилиндр бесконечно малой высоты, основания которого параллельны границе
раздела двух диэлектриков.
В соответствии с теоремой Гаусса, считая электрическое поле однородным, мы вправе записать*:
и
.
Отсюда следует, что
.
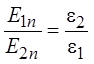Таким образом, на границе раздела скачком изменяется нормальная составляющая вектора напряжённости и не изменя-ется нормальная составляющая вектора электрического смещения.
Вследствие этого силовые линии на границе раздела двух диэлектриков изменяют направление**. Действительно,
Е1t = Е2t,
e1Е1n = e2Е2n.
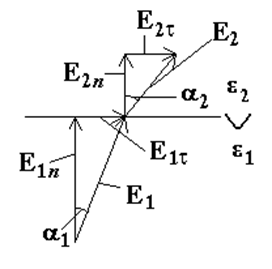Из рисунка видно, что 
.
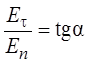Выражая тангенс угла наклона силовых линий в каждом из диэлектриков, получим:
, 
,
.
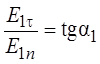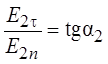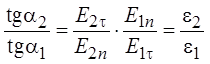Таким образом, в среде с бóль-шей диэлектрической проницаемостью (e2 >e1) силовые линии увеличивают наклон (см. рисунок)
_______________________
* Мы не будем здесь подробно описывать математические преобразования: они просты и практически одинаковы с рассмотренными перед этим.
** Если силовые линии перпендикулярны границе раздела, то их направление не изменяется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
