Полный поток через оба торца цилиндра Ф = 2Еpr2.
Суммарный заряд, охваченный
поверхностью цилиндра, равен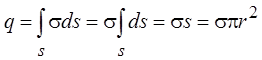 
.
Отсюда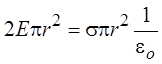 
и 
.
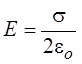Полученное выражение показывает, что напряжённость поля, созданного бесконечной равномерно заряженной плоскостью, прямо пропорциональна поверхностной плотности заряда и не зависит от расстояния.
Обратите внимание: в этом случае напряжённость элект-рического поля на любых расстояниях от плоскости одинакова!
Пусть имеются две параллельные плоскости, заряды которых одинаковы по величине и противоположны по знаку. Поверх-ностные плоскости зарядов соответственно равны s и -s.
Напряжённость поля, созданного двумя плоскостями, в соответствии с принципом суперпозиции может быть найдена как векторная сумма напряжённостей, созданных каждой плоскостью в отдельности, Е = Е1 + Е2.
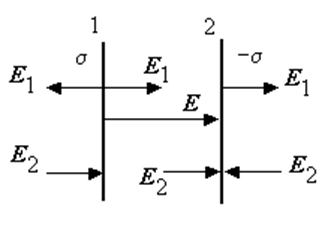Напряжённости полей,
созданных каждой из плоскостей, во всех точках пространства одинаковы по
величине и противоположны по направ-лению (так как заряды плоскостей одинаковы
по величине и противопо-ложны по знаку).
Это означает, что
напря-жённость поля между плас-тинами равна удвоенной напряжённости поля,
созданного одной пласти-ной,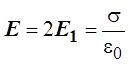 
.
Напряжённость поля вне пластин равна нулю.
Пусть имеется сфера радиуса rо, по которой равномерно распределён заряд q.
Из симметрии системы следует, что поле должно быть сим-метрично относительно центра заряженной сферы. Следова-тельно, вектор Е во всех точках пространства направлен параллельно радиальным прямым и на равных расстояниях от центра сферы модули Е одинаковы.
В этом случае в качестве поверхности интегрирования целесообразно выбрать сферическую поверхность, центр которой совпадает с центром заряженной сферы.
Пусть радиус сферической поверхности меньше, чем радиус заряженной сферы. В этом случае суммарный заряд, охваченный поверхностью, равен нулю (так как внутри сферы зарядов нет, все заряды расположены на её поверхности).
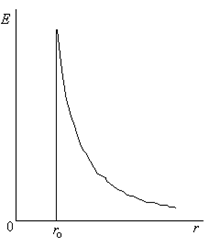
Это означает, что внутри заряженной сферы поток вектора напряжённости через поверхность, радиус которой ro>r>0, равен нулю.
Площадь поверхности отлична от нуля, поэтому поток может быть равен нулю лишь в том случае, если напряжённость поля внутри сферы равна нулю.
Следовательно, напряжённость электрического поля внутри заряженной сферы равна нулю Е(ro ³ r > 0) = 0.
Пусть радиус поверхности интегрирования больше радиуса заряженной сферы. В этом случае суммарный заряд, охваченный поверхностью, равен заряду сферы q.
Если единичный вектор n направлен наружу от поверхности, то угол между n и Е во всех точках равен нулю (или 180о, если заряд сферы отрицательный).
Отсюда следует, что 
.
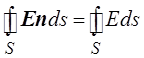Поскольку модуль вектора Е
во всех точках выбранной поверхности одина-ков и площадь сферы равна 
, по-стольку поток вектора напряжённости
электрического поля
.
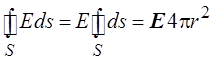В соответствием с теоремой Гаусса поток вектора Е пропорционален сумме зарядов, охваченных поверхностью:
.
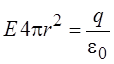Следовательно, напряжённость электрического поля, создан-ного заряженной сферой снаружи от неё, равна
.
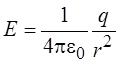Обратите внимание на то, что поле вне заряженной сферы совпадает с полем точечного заряда q (см. разд. 1.3).
Если заряд движется в электростатическом поле, то кулоновская сила совершает работу.
Найдём величину работы, совершаемой при перемещении заряда в электростатическом поле.
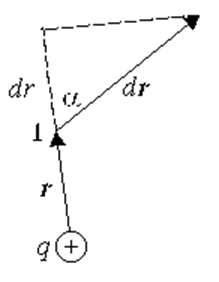Допустим, что заряд qо
перемещается на dr из точки 1 в электрическом поле точечного заряда
q.
При этом совершается элементарная работа, равная dА = Fdr.
Учитывая, что кулоновская
сила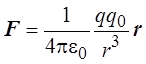 
, получаем
dА =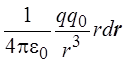 
.
Из рисунка видно, что rdr = rdr. Поэтому
.
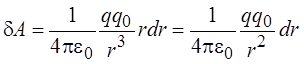На конечном перемещении из точки 1 в точку 2 работа электростатических сил
.
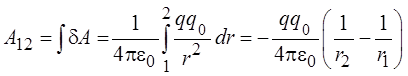Таким образом, работа по перемещению заряда в электростатическом поле зависит от величины заряда (зарядов), создающего поле, величины перемещаемого заряда и его начального и конечного положений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.