где I – сила тока в цепи, U – напряжение на концах цепи, R – сопротивление цепи.
Это выражение принято называть законом Ома для участка цепи.
Сопротивление цепи есть коэффициент, связывающий на-пряжение в цепи и силу тока, возникающего в цепи за счёт напряжения U.
Поскольку размерности силы
тока и напряжения не совпадают, R является размерным коэффициентом.
Размерность сопротивления можно получить из закона Ома: [R] = [U]/[I]
=
= В/А = Ом.
Величина сопротивления цепи при постоянной температуре зависит от размеров и формы проводников цепи, от материала, из которого проводники изготовлены. Увеличение температуры у большинства проводников вызывает возрастание сопротивления.
Для однородного по составу
проводника постоянной длины и сечения сопротивление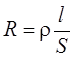 
, где r – удельное сопротивление
проводника*; l – длина проводника, S – площадь поперечного сечения проводника.
Закон Ома для участка цепи может быть записан в диф-ференциальной форме
,
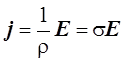где j – плотность тока в проводнике; r – удельное сопротивление проводника; s – удельная электрическая проводимость провод-ника; Е – напряжённость электрического поля в проводнике.
Если участок цепи неоднороден, то кроме электростатических сил на свободные заряды действуют и сторонние, тогда
J = sE + sE*.
Это выражение представляет собой закон Ома в диф-ференциальной форме для неоднородного участка цепи.
В интегральной форме это выглядит так:
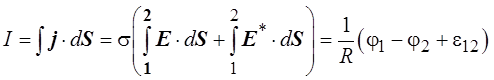
и
где j1 – j2 – разность потенциалов на концах участка цепи.
Последнее выражение представляет собой закон Ома для неоднородного участка цепи в интегральной форме.
Если неоднородная цепь замкнута, то j1 = j2 (так как концы участка цепи соединены между собой) и закон Ома принимает следующий вид:
,
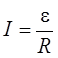где R – суммарное сопротивление однородного участка цепи и внутреннего сопротивления источника ЭДС.
Это выражение представляет собой закон Ома для замкнутой цепи.
___________________________
* Удельное сопротивление зависит от материала проводника; размерность удельного сопротивления – Ом×м.
Рассмотрим участок цепи, напряжение на концах которой равно U.
В рассматриваемой цепи будет протекать электрический ток, сила которого, в соответствии с законом Ома, равна U/R.
По определению (см. разд. 2.1), напряжение равно работе электростатических и сторонних сил по перемещению единичного заряда в электрической цепи. Следовательно, при протекании тока кулоновские и сторонние силы, действующие на заряды в рассматриваемом участке, совершат работу
.
Эту работу называют работой электрического тока.
Если ток постоянный, то q = It, где I – сила тока, t – время, в течение которого в проводнике течёт ток. В этом случае работа тока может быть рассчитана по формуле
.
Поскольку 
, постольку работа тока
.
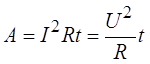Таким образом, работа тока
может быть рассчитана с помощью нескольких формул. Какое именно выражение
следует использовать в конкретной задаче, определяется её условием. Например,
если в условии дана сила тока и разность потенциалов на концах однородного
участка цепи, то 
, если же известны сила тока и
сопротивление цепи, то 
.
Мощность есть работа,
совершённая за единицу времени: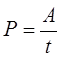 
. Поэтому мощность тока
можно рассчитать по следующим формулам:
.
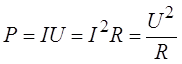Если проводник с током неподвижен и ток не вызывает химических реакций, то вся работа идёт на увеличение внут-ренней энергии проводника, т. е. на его нагрев.
Другими словами – при протекании тока в проводнике выделяется тепло
.
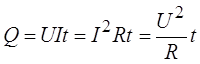В 1841 г. англичанин Джеймс П. Джоуль и независимо от него в 1842 г. русский физик Эмилий Христианович Ленц, обобщая результаты своих экспериментов, получили именно такое выражение для расчета количества тепла, выделяемого про-водником при протекании в нём тока. Поэтому последнее выражение принято называть законом Джоуля–Ленца.
Если сила тока изменяется с течением времени, то количество тепла, выделяющееся в цепи, можно рассчитать с помощью следующих выражений:
.
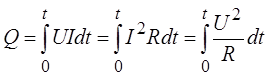Закон Джоуля–Ленца может быть записан и в дифференциальной форме:
,
где v – удельная тепловая мощность тока (это количество тепла, выделяющееся за единицу времени в единице объёма проводника).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.