




































Закон распределения в любой его форме является исчерпывающей характеристикой вероятностного поведения случайного объекта (величины, вектора, функции). Поскольку задача его определения достаточно сложна, на практике часто определяются лишь числовые характеристики, основными из которых являются математическое ожидание и дисперсия. Для случайных векторов характеристикой рассеяния является корреляционная матрица.
Следует отметить, что решение такой более упрощённой задачи имеет большую практическую ценность, так как во многих случаях знать закон распределения не требуется. Кроме того, часто на основе каких-то априорных предположений вид закона распределения исследуемого случайного объекта известен и для его полного описания достаточно определить лишь параметры.
Как уже отмечалось, задача оценивания параметров распределения, в частности числовых характеристик, сводится к отысканию таких статистик (функций случайной выборки), которые могут служить наилучшими в каком-то смысле оценками истинных значений параметров. Все рассматриваемые оценки должны проверяться на наличие у них основных необходимых свойств: несмещённости, состоятельности и эффективности.
Пусть имеется случайная величина ![]() ,
математическое ожидание которой
,
математическое ожидание которой ![]() неизвестно. Над
случайной величиной проведено n независимых
опытов (наблюдений). По их результатам x1, x2,…, xn требуется найти
состоятельную, несмещённую и эффективную оценку
неизвестно. Над
случайной величиной проведено n независимых
опытов (наблюдений). По их результатам x1, x2,…, xn требуется найти
состоятельную, несмещённую и эффективную оценку ![]() параметра
параметра
![]() , т.е. найти функцию
, т.е. найти функцию
![]() .
.
В качестве оценки математического ожидания (среднего
значения) случайной величины ![]() могут приниматься
различные характеристики случайной выборки. Все общие методы статистического
оценивания дают в качестве наилучшей точечной оценки математического ожидания
случайной величины её статистическое среднее. Однако при нахождении оценки
математического ожидания, удовлетворяющей требованиям состоятельности,
несмещённости и эффективности, следует различать равноточные и неравноточные
наблюдения (однородные и неоднородные опыты).
могут приниматься
различные характеристики случайной выборки. Все общие методы статистического
оценивания дают в качестве наилучшей точечной оценки математического ожидания
случайной величины её статистическое среднее. Однако при нахождении оценки
математического ожидания, удовлетворяющей требованиям состоятельности,
несмещённости и эффективности, следует различать равноточные и неравноточные
наблюдения (однородные и неоднородные опыты).
Статистическое (выборочное) среднее или статистическое математическое ожидание случайной величины находится по формуле
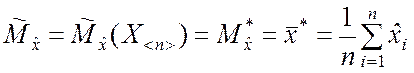 . (5.1.1)
. (5.1.1)
Поскольку наблюдения равноточны, то случайные величины ![]() по существу представляют собой
«экземпляры» одной и той же случайной величины
по существу представляют собой
«экземпляры» одной и той же случайной величины ![]() и,
следовательно, имеют один и тот же закон распределения с числовыми
характеристиками:
и,
следовательно, имеют один и тот же закон распределения с числовыми
характеристиками:
![]() ;
; ![]()
![]() ,
, ![]() .
.
Покажем, что оценка ![]() удовлетворяет
всем трём общим требованиям.
удовлетворяет
всем трём общим требованиям.
1. Из выражения (5.1.1) следует, что
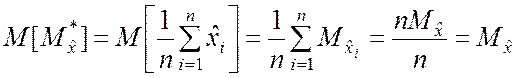 .
.
Таким образом, ![]() является несмещённой
оценкой параметра
является несмещённой
оценкой параметра ![]() .
.
2. Согласно теореме Чебышева среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к её математическому ожиданию
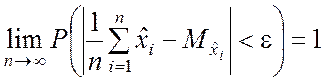 .
.
Следовательно, статистическое среднее ![]() есть
состоятельная оценка параметра
есть
состоятельная оценка параметра ![]() .
.
3. Согласно выражению (5.1.1) дисперсия статистического среднего
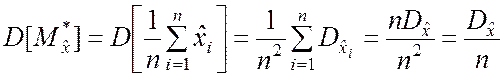 (5.1.2)
(5.1.2)
с ростом объёма n выборки
неограниченно убывает и, следовательно, ![]() асимптотически
эффективная оценка
асимптотически
эффективная оценка ![]() . Доказано, что если случайная
величина
. Доказано, что если случайная
величина ![]() подчинена нормальному закону
распределения, то при любых n дисперсия (5.1.2)
будет минимально возможной. В таком случае
подчинена нормальному закону
распределения, то при любых n дисперсия (5.1.2)
будет минимально возможной. В таком случае ![]() является
эффективной оценкой математического ожидания
является
эффективной оценкой математического ожидания ![]() .
.
Следовательно, ![]() – это подходящее
значение
– это подходящее
значение ![]() :
:
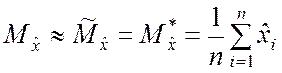 . (5.1.3)
. (5.1.3)
П р и м е р 5.1. В условиях примера 4.1 найти
оценку математического ожидания случайной величины ![]() .
.
▼ Согласно формуле (5.1.3)
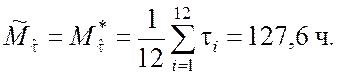
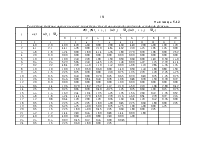
Случайная выборка, приведённая в табл.4.3, была получена при
наблюдении случайной величины ![]() , математическое
ожидание которой
, математическое
ожидание которой ![]() Сравнительно невысокая точность
полученной оценки обусловлена малым объёмом выборки, но ни в коей мере не
способом её вычисления. ▲
Сравнительно невысокая точность
полученной оценки обусловлена малым объёмом выборки, но ни в коей мере не
способом её вычисления. ▲
Если объём n выборки достаточно велик, то вычисления по формуле (5.1.3) оказываются громоздкими. Задачу можно упростить, если использовать данные интервального вариационного ряда, т.е. полагать
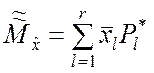 , (5.1.4)
, (5.1.4)
где ![]() – представитель (середина) l-го разряда вариационного ряда;
– представитель (середина) l-го разряда вариационного ряда; ![]() –
частота попадания вариантов xi
случайной величины
–
частота попадания вариантов xi
случайной величины ![]() в l-й
разряд.
в l-й
разряд.
Значение оценки ![]() , определяемое по
формуле (5.1.4), оказывается приближённым, однако с ростом n
(а, следовательно, и r) точность данной формулы
возрастает.
, определяемое по
формуле (5.1.4), оказывается приближённым, однако с ростом n
(а, следовательно, и r) точность данной формулы
возрастает.
П р и м е р 5.2. В условиях примера 4.2 найти
приближённое значение оценки ![]() математического
ожидания
математического
ожидания ![]() случайной величины
случайной величины ![]() .
.
▼ Используем данные табл.4.7. По формуле (5.1.4) получим
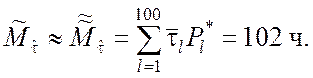 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.