Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 15

Числовые характеристики , ,  случайной функции  зависят от параметра t, следовательно, от него зависят как оценки , , , так и характеристики их качества – доверительные интервалы:

                                            ;             (5.4.14)

                                             ;              (5.4.15)

                                        ,        (5.4.16)

а также доверительные вероятности:

                                   ;    (5.4.17)

                                    ;     (5.4.18)

                            ,                                                        (5.4.19)

Во всех приведённых выражениях n – это число наблюдаемых реализаций случайной функции . Если случайная функция  стационарна, то выражения (5.4.14)–(5.4.19) упрощаются и принимают следующий вид:

                                                ;                             

                                                 ;                             

                                             ,                         

                                         ;                     

                                          ;                      

                                   ,               

где T – продолжительность наблюдения случайной функции .

5.4.4. Потребный объём наблюдений

При оценивании числовых характеристик нестационарной случайной функции задача состоит в определении потребного числа n её реализаций x_i(t), . Поскольку все числовые характеристики случайной функции, а также характеристики  (5.4.14) – (5.4.19)  качества оценивания зависят от параметра t, то от него будет зависеть и потребный объём n выборки реализаций:

                                                ;                 (5.4.20)

                                               ;                (5.4.21)

                                             .              (5.4.22)

Выражениями (5.4.20)–(5.4.22) определяется потребный объём реализаций случайной функции для оценки соответственно математического ожидания, дисперсии и корреляционной функции. Из данных выражений следует, что оценивание числовых характеристик случайной функции для различных её сечений может потребовать различного числа реализаций. Такое требование практически неосуществимо. Поэтому требуемый объём n_k,  k = 1, 2, 3 определяется как 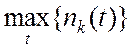, соответствующий минимуму дисперсии оценки k-й числовой характеристики случайной функции:

                                                 ;                             

                                                ;

                                             .

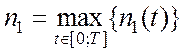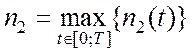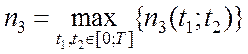При оценивании числовых характеристик стационарной случайной функции  наблюдается всего одна её реализация u(t). Поэтому здесь возникает вопрос о длительности наблюдения T, потребной для оценивания характеристик случайной функции с заданной точностью I или e и надёжностью b.

Поскольку случайная функция  стационарна, то все её сечения распределены одинаково. По этой причине последовательность значений u(t_j),  наблюдаемой реализации u(t) случайной функции  может интерпретироваться как однородная выборка u(t₁), u(t₂),…,u(t_m), элементы которой принадлежат одной и той же генеральной совокупности. Теперь задача состоит в определении потребного объёма n этой выборки.

По методикам, изложенным в §§ 5.1 – 5.3, получим соотношения:

                                                      ;

                                                     ;

                                        .

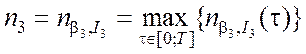Так как наблюдается всего одна реализация случайной функции, то потребное число n её измерений определяется следующим соотношением:

                                               n = max{n₁; n₂; n₃}.               (5.4.23)

Поскольку регистрация значений реализации u(t) стационарной случайной функции  обычно производится через равные промежутки времени длительностью h, то потребная длительность наблюдения реализации определяется равенством

                                                         T = nh,

где n находится из соотношения (5.4.23).