Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 12

▲

5.4.2. Стационарные случайные функции

По определению, случайная функция  является стационарной (в широком смысле), если её математическое ожидание и дисперсия постоянны, а корреляционная функция зависит лишь от расстояния между сечениями случайной функции:

                                         ;

                                         ;

                            .

Класс стационарных случайных функций достаточно многообразен. Однако в практическом отношении наибольший интерес представляют стационарные случайные функции, обладающие эргодическим свойством, для которых одна реализация достаточно большой продолжительности содержит о случайной функции столько же информации, сколько её содержит и множество реализаций той же суммарной продолжительности. Другими словами, каждая из реализаций эргодической стационарной случайной функции является представителем всего их ансамбля. Как отмечено в работе [12], следует различать эргодические свойства случайных функций по отношению к моментам их распределения различных порядков. При этом под эргодичными обычно понимаются случайные функции, обладающие такими свойствами по отношению к моментам первого и второго порядков, т.е. к математическому ожиданию и корреляционной функции (следовательно, и к дисперсии). Далее рассматриваются только такие случайные функции.

Оценки числовых характеристик эргодичных случайных функций могут быть приближённо определены не как средние по множеству реализаций, а как средние по времени T наблюдения одной реализации по следующим формулам:

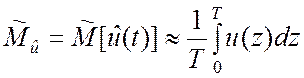                               ,   t Î [0; T];  (5.4.6)

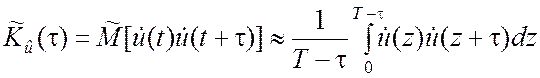,   t Î [0; T–t];                                                         (5.4.7)

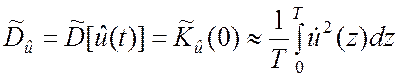,   t Î [0; T],                                                         (5.4.8)

где  .

Обоснованием применимости формул  (5.4.6) – (5.4.8)  служит тот факт, что для эргодичных стационарных случайных функций средние во времени оценки сходятся по вероятности к оцениваемым ими характеристикам , , .

Из выражений  (5.4.6) – (5.4.8)  видно, что для их практического применения требуется интегрировать ряд функций от реализации u(t) случайной функции . Чаще всего на практике для нахождения оценок (5.4.6) – (5.4.8) используется следующая методика.