Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

i	xi	i	xi	i	xi	i	xi	i	xi
1	10,5	5	10,4	9	10,3	13	10,5	17	10,8
2	10,8	6	10,6	10	10,8	14	10,7	18	10,7
3	11,2	7	10,9	11	10,6	15	10,8	19	10,9
4	10,9	8	11,0	12	11,3	16	10,9	20	11,0

1. Найти оценку  математического ожидания величины  и построить доверительный интервал, соответствующий доверительной вероятности b = 0,8.

2. Определить доверительную вероятность b для математического ожидания случайной величины , если максимальная вероятная погрешность e_b =0,07.

▼ 1. В соответствии с выражением (5.1.1) находим оценку математического ожидания

                                             .

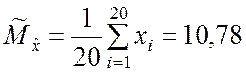По первой формуле (5.2.14) находим оценку дисперсии

                                .

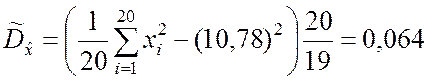Оценка среднего квадратического отклонения

                                       .

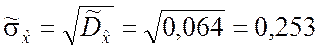При заданном b = 0,8 величина t_b = 1,282 (см. приложение 4), тогда максимальное вероятное отклонение математического ожидания найдём по формуле (5.1.16), что составит

                                    .

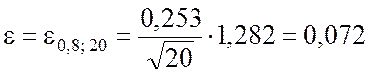Выражение (5.1.17) даёт следующий результат:

                   I_0,8; 20 = [10,78–0,072;  10,78+0,072] = [10,71; 10,85].

2. В соответствии с соотношением (5.1.15) находим

  .

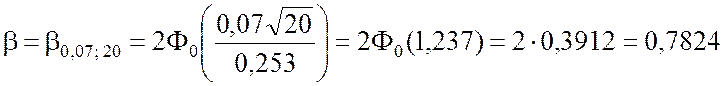Значение функции F₀(x) найдены в приложении 2.

▲

П р и м е р 5.7. Габаритный размер  деталей измеряется методом, который характеризуется дисперсий  = 0,064. Определить потребный объём выборки, чтобы максимальная вероятная погрешность e оценки среднего размера деталей не превосходила 0,06 при доверительной вероятности b = 0,93.

▼ Для b = 0,93 в приложении 4 находим t_b = 1,810. Тогда из выражения (5.1.18) получаем

                                          .

▲

5.2.3. Качество оценивания дисперсии

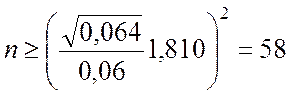Качество оценивания дисперсии  характеризуется доверительным интервалом

                                                  

и доверительной вероятностью

                                           .

При оценивании дисперсии различают случаи известного и неизвестного математического ожидания (см. пп. 5.2.1, 5.2.2). Рассмотрим второй, наиболее распространённый случай. При неизвестном  состоятельная, несмещённая и асимптотически эффективная оценка дисперсии определяется равенством (5.2.9).

При достаточно большом объёме выборки распределение оценки (5.2.9) будет близким к нормальному с параметрами (5.2.10). Следовательно, доверительная вероятность для дисперсии будет приближённо определяться соотношением

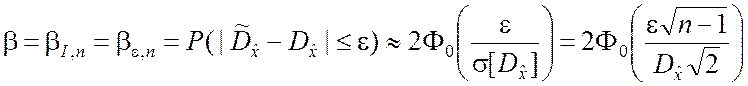,                                                       (5.2.15)

где e = e_b,n – максимальная с вероятностью b абсолютная погрешность оценки  дисперсии .

Выражаем e из уравнения (5.2.15) и в результате получим

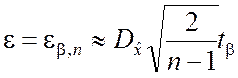                                             ,              (5.2.16)

откуда доверительный интервал

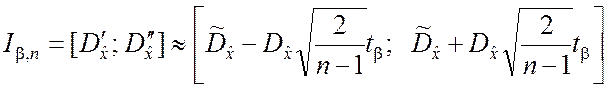                   .                                                        (5.2.17)

Выражения (5.2.15) – (5.2.17) были получены в предположении, что дисперсия  известна. В действительности известна лишь её оценка , которая только и может фигурировать в этих формулах. С учётом сказанного будем иметь

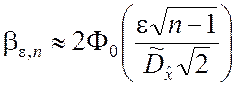                                             ;              (5.2.18)

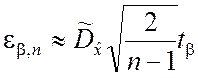                                                ;                 (5.2.19)

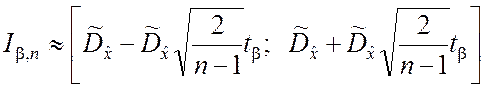                            .         (5.2.20)

Как видно из выражения (5.2.20), доверительный интервал для дисперсии  оказывается симметричным относительно оценки . При этом его ширина зависит от значения  (рис.5.2).

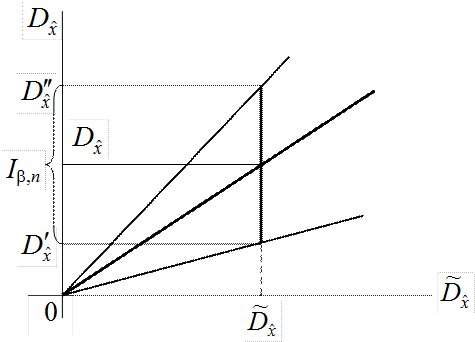
Рис.5.2. Доверительный интервал для дисперсии