Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 13

Пусть на интервале времени [0; T] наблюдалась реализация эргодичной стационарной случайной функции, значения которой u(t_j) в ряде равноотстоящих опорных моментов времени  t_j = 0,5h + kh, ,  зарегистрированы и сведены в табл.5.10.

Таблица 5.10

Значения реализации эргодичной стационарной функции в выбранные моменты времени

t	t1	t2	×××	tj	×××	tm
u(t)	u(t1)	u(t2)	×××	u(tj)	×××	u(tm)

Требуется по данным этой таблицы определить оценки , ,  числовых характеристик , ,  случайной функции

Интервал [0; T] наблюдения случайной функции  разбивается на m равных подынтервалов длиной h = T/m, расположенных симметрично относительно опорных моментов времени t₁, t₂,…, t_m  (рис.5.4).

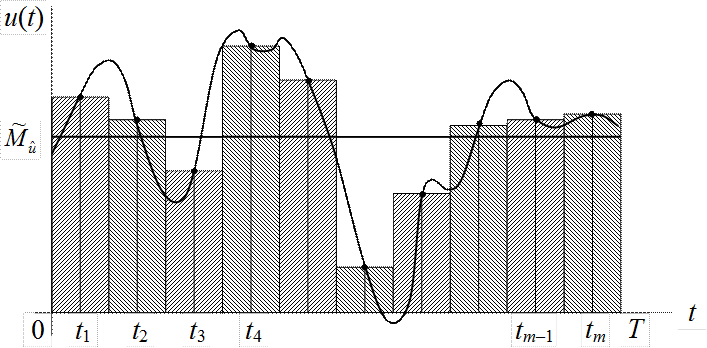
Рис.5.4. Реализация эргодичной стационарной случайной функции

Далее предполагается, что в пределах подынтервала                       [t_j–0,5h; t_j+0,5h]  функция, описывающая  реализацию случайной функции, постоянна:

                   u(t) = u(t_j) = const,   t Î [t_j – 0,5h;  t_j + 0,5h],  ,

Если h достаточно мало, то можно приближённо полагать, что

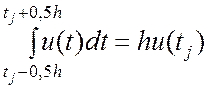                                       ,   .         (5.4.9)

Суммирование результатов (5.4.9)  по  j  даёт

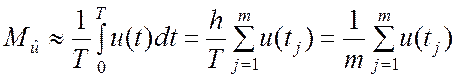                              .                                                        (5.4.10)

Несложно заметить, что выражение (5.4.10) реализует процедуру численного интегрирования по формуле прямоугольников.

Аналогично вычисляется и оценка корреляционной функции для значений аргумента

                                                     .

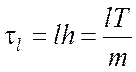Поскольку в выражении (5.4.7) длина интервала интегрирования

                                           ,

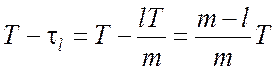то, поделив его на  m – l  равных участков и вынося на каждом из них за знак интеграла среднее значение функции , получим

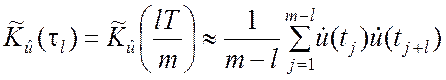,   ,                                                        (5.4.11)

где L = m/4  [2].

При t = 0 формула (5.4.11) даёт

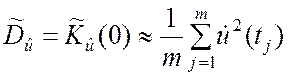                                          .          (5.4.12)

Вычисления по формуле (5.4.11) ведутся последовательно для  l = 0, 1, 2,… вплоть до таких значений l_k, при которых функция  становится практически равной нулю или начинает совершать незначительные колебания около нуля. По полученным точкам может быть построен приближённый график корреляционной функции  (рис.5.5).

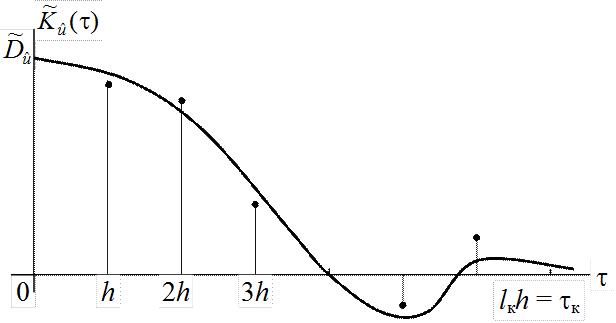
Рис.5.5. Приближённый график корреляционной функции

На представленном рисунке через t_к обозначена длина интервала корреляции случайной функции , т.е. наименьшее расстояние между сечениями случайной функции, на котором корреляция между ними практически отсутствует (t_к = l_кh).

П р и м е р 5.12. В табл.5.11 приведены результаты наблюдения эргодичной стационарной случайной функции  на интервале времени продолжительностью T = 28 с с периодичностью h = 1 с в моменты времени t_j, .

Таблица 5.11

Реализация эргодичной стационарной случайной функции

tj, c	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t11	t12	t13	t14
u(tj)	4,0	4.1	3,8	2,0	1,0	–0,3	–0,2	1,0	3,5	2,5	2,6	2,0	0,6	2,5
tj, c	t15	t16	t17	t18	t19	t20	t21	t22	t23	t24	t25	t26	t27	t28
u(tj)	3,3	3,8	1,2	0,5	–0,5	0,5	3,2	4,0	2,3	0,5	2,4	3,2	2,0	0,5

Требуется определить оценки числовых характеристик функции .

▼ Необходимые вычисления производятся по формулам (5.4.10–(5.4.12). Результаты расчётов оформлены в виде табл.5.12, наглядно иллюстрирующей все этапы решения задачи.