Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

                                               

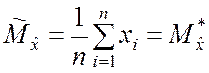
Получим результат как и в пп.5.1.1 – оценкой математического ожидания случайной величины  является её статистическое среднее .

П р и м е р 5.3. Дальность  до центра масс ракеты измеряется тремя методами, точность которых характеризуется средними квадратическими отклонениями  = 0,2 км,  = 0,5 км,  = 1 км. Измерения дальности  этими методами дали следующие результаты: x₁ = 10,0 км; x₂ = 9,5 км;  x₃ = 10,8 км.

Найти оценку  математического ожидания  дальности  и среднее квадратическое отклонение  этой оценки.

▼ По условию задачи

      ,   ,   .

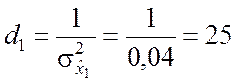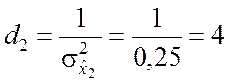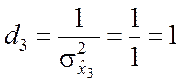Далее согласно равенствам (5.1.9)

                                      ,    ,    

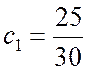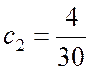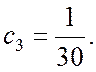
По формуле (5.1.5) получаем

                            .

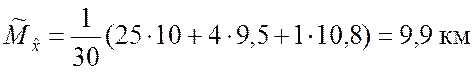В соответствии с выражением (5.1.11)

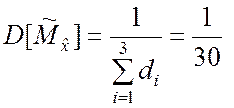                    км²,    .

▲

5.1.3. Качество оценивания математического ожидания

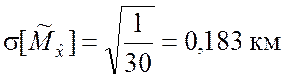Качество статистического оценивания математического ожидания при заданном объёме n выборки определяется доверительным интервалом

                                                                   (5.1.12)

и доверительной вероятностью

                                     .     (5.1.13)

Как указывалось в § 3.2, процедура построения доверительного интервала зависит, с одной стороны, от характера распределения наблюдаемого признака  и, как следствие, от распределения оценки , а с другой – от объёма n случайной выборки . Кроме того, и в первую очередь, она зависит от типа статистики , используемой в качестве  оценки  математического ожидания. В п.п. 5.1.1 и 5.1.2 применялись линейные статистики в виде средневзвешенного элементов выборки.

В случае равноточных независимых наблюдений наилучшей (по трём критериям, см. § 3.1) оценкой математического ожидания является статистическое математическое ожидание (5.1.1). При этом, если наблюдаемая случайная величина  подчинена нормальному закону распределения, то при любом n оценка  будет иметь нормальное распределение с параметрами

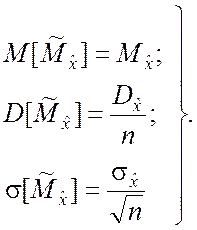                                                                  (5.1.14)

Наряду с этим оценка  асимптотически нормальна, т.е. при n ® ¥ для любого распределения признака  распределение оценки  приближается к нормальному с параметрами, определяемыми равенствами (5.1.14). Данное утверждение вытекает из предельной теоремы Ляпунова.

Тогда доверительная вероятность (5.1.13) будет определяться отношением

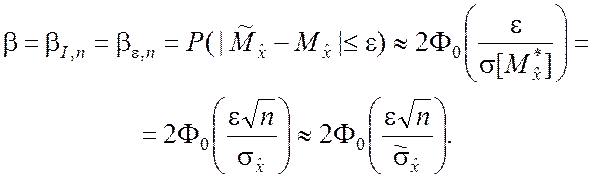                                                                            (5.1.15)

Первое приближённое равенство в (5.1.15) обусловлено отличием закона распределения признака  от нормального, а второе – заменой неизвестного  его оценкой . При нормальном распределении  и известном  соотношение (5.1.15) становится точным.

Разрешив (5.1.15) относительно e, получим

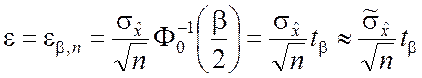                                , (5.1.16)

откуда находим интервал  (5.1.12):

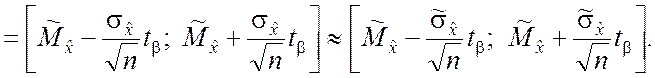                                                                     (5.1.17)

Из соотношения (5.1.17) видно, что при большом объёме выборки доверительный интервал для  симметричен и полностью определяется его оценкой и максимальной с вероятностью b абсолютной погрешностью e_b,n. На рис.5.1 дана геометрическая интерпретация соотношения (5.1.17).

Из уравнения (5.1.16) выражаем n, при этом будем иметь

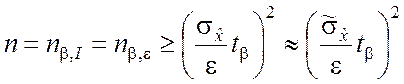                                 .  (5.1.18)

Формулой (5.1.18) определяется потребный объём выборки для оценивания математического ожидания случайной величины .

5.2. Оценивание дисперсии и среднего квадратического отклонения случайной величины

Над случайной величиной  производится n независимых равноточных наблюдений. Требуется по результатам эксперимента определить состоятельные и несмещённые оценки  и  характеристик рассеяния  и  случайной величины , т.е. найти

                                    и  .

Ограничимся рассмотрением наиболее важного для практики случая, когда случайная величина  подчинена нормальному закону распределения с параметрами  и .