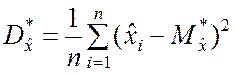Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

                                             ,                (5.2.6)

и исследуем её свойства.

1. По аналогии со случаем, когда математическое ожидание известно, можно показать состоятельность оценки (5.2.6).

2. Преобразуем выражение (5.2.6)

                                                 

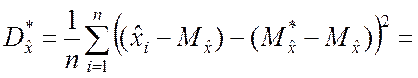
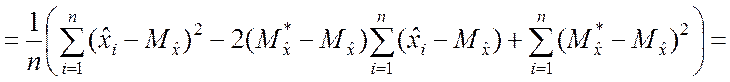
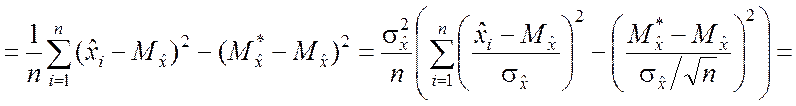
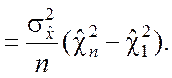
Поскольку случайные величины  и  являются функциями одной и той же выборки, то они зависимы. Причём их зависимость такова, что разность этих случайных величин оказывается подчинённой закону распределения хи-квадрат с  n – 1  степенями свободы. Таким образом

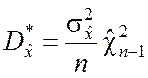                                                    ,                      (5.2.7)

откуда

                                 .             

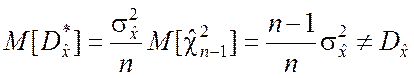Следовательно, статистическая дисперсия  оказывается смещённой оценкой параметра . Для исправления оценки  её достаточно умножить на коэффициент n(n–1). С ростом объёма n выборки указанный коэффициент стремится к единице, поэтому при достаточно больших n смещённостью оценки  можно пренебречь.

3. Поскольку

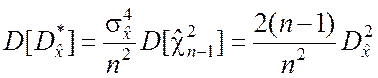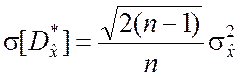,    ,                                                         (5.2.8)

то при n ® ¥ имеет место . Результат, полученный на основе анализа выражения (5.2.8), свидетельствует об асимптотической эффективности оценки .

Итак, при n ® ¥ исправленная статистическая дисперсия

                                         (5.2.9)

является подходящим значением дисперсии  случайной величины . С уменьшением объёма n выборки эффективность этой оценки несколько падает.

Оценка (5.2.9) имеет следующие числовые характеристики:

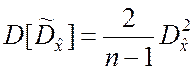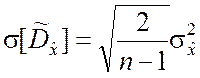;   ;   .                                                        (5.2.10)

Вычисление дисперсии  связано со сложными выкладками, поэтому её выражение приведено без вывода.

При большом объёме n выборки приближённое значение оценки  можно вычислять по формуле

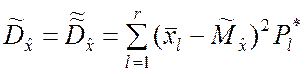                                        .         (5.2.11)

Перейдём к отысканию оценки для среднего квадратического отклонения  случайной величины  в случае неизвестного математического ожидания. Указанная оценка определяется по формуле

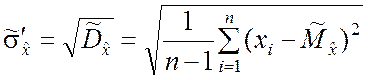                                    .     (5.2.12)

Проанализируем свойства оценки (5.2.12).

1. Из вышеизложенного следует, что данная оценка состоятельна и асимптотически эффективна.

2. Согласно выражениям (5.2.7) и (5.2.9) имеем

                                                 .                             

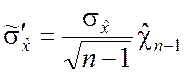Поэтому

                     

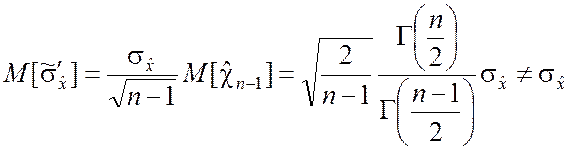
и, следовательно, (5.2.12) является смещённой оценкой . Для исправления данной оценки её достаточно умножить на коэффициент

                                            .

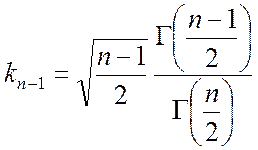Полученная при этом функция случайной выборки

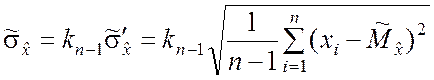                                (5.2.13)

будет состоятельной, несмещённой и асимптотически эффективной оценкой среднего квадратического отклонения  случайной величины .

Подходящее значение  можно получить и непосредственно, используя статистическую дисперсию (5.2.6). Для исправления получаемой при этом оценки 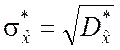 её необходимо умножить на коэффициент

                                                ,

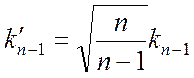т.е. величина

                                       

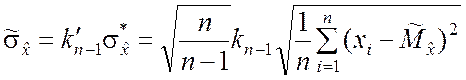
является состоятельной, несмещённой и асимптотически эффективной оценкой.

В заключение отметим, что поскольку известное соотношение для дисперсии

                                               

справедливо и для её оценки, т.е.

                                               ,

то формулам (5.2.1), (5.2.4) и (5.2.9), (5.2.11) соответственно можно придать более удобный для практического использования вид:

                                                                

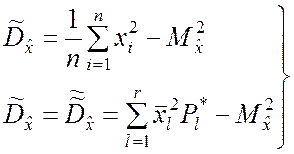
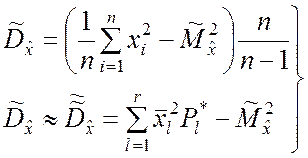                                                  (5.2.14)

П р и м е р 5.6. Производятся измерения одного из габаритных размеров  однотипных деталей. Данные измерений сведены в табл.5.2.

Таблица 5.2

Результаты измерений размера деталей