Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

При решении поставленной задачи следует различать два случая – когда параметр  известен и когда он неизвестен.

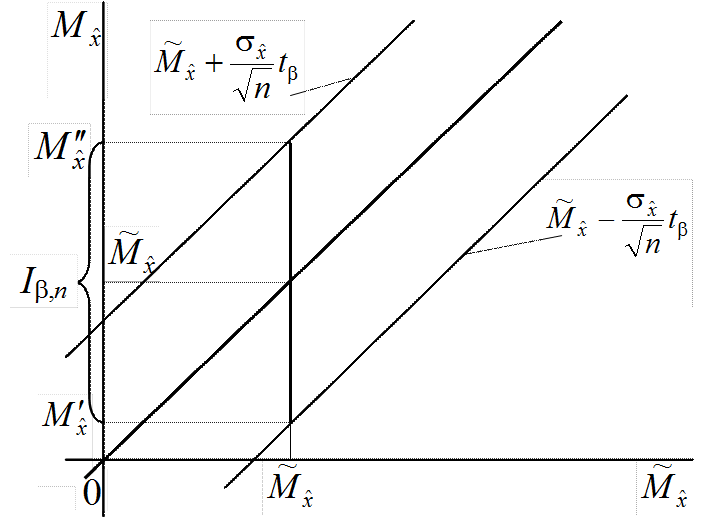
Рис.5.1. Доверительный интервал для математического ожидания

5.2.1. Оценивание дисперсии и среднего квадратического отклонения при известном математическом ожидании

Вводим случайную величину

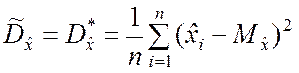                                         ,            (5.2.1)

которая называется дисперсией случайной выборки или статистической, выборочной дисперсией. Установим некоторые из свойств случайной величины (5.2.1).

1. Преобразуем  к виду

                                     ,

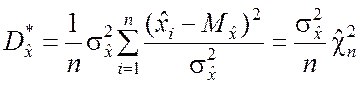т.е.  является линейной функцией от случайной величины , подчинённой хи-квадрат распределению (распределению К. Пирсона) с n степенями свободы. Следовательно

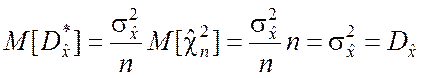                                .   (5.2.2)

Таким образом,  – несмещённая оценка .

2. Поскольку

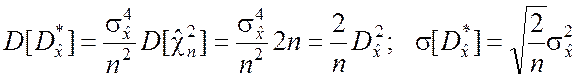                     ,                                                         (5.2.3)

то при n ® ¥ имеет место  ® 0. Иначе, дисперсия  случайной выборки асимптотически эффективная оценка .

3. Как следует из (5.2.2) и (5.2.3), случайная величина  имеет числовые характеристики

                           .

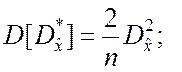
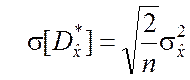Поскольку

                                                  ,

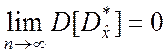то оценка  является состоятельной.

Итак, при n ® ¥ дисперсия случайной выборки (5.2.1) представляет собой подходящее значение дисперсии  случайной величины . При малых  n она в общем случае не вполне эффективна.

П р и м е р 5.4. Полагая  = 100 ч, в условиях примера 4.1 найти оценку  дисперсии   случайной величины .

▼ Используем данные табл.4.3 и по формуле (5.2.1) получаем

                                .

▲

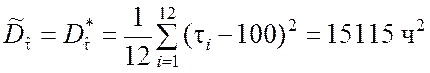Если объём n выборки достаточно велик, то для вычисления оценки  можно пользоваться приближённой формулой

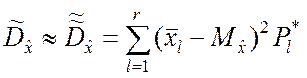                                        ,           (5.2.4)

где и  имеют тот же смысл, что и в формуле (5.1.4).

П р и м е р 5.5. Полагая  = 100 ч, в условиях примера 4.2 найти приближённое значение оценки  дисперсии  случайной величины .

▼ Используя табл.4.7, по формуле (5.2.4) получаем

                                 .             

▲

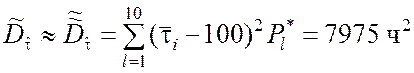Теперь найдем оценку среднего квадратического отклонения . Формула для определения статистического среднего квадратического отклонения имеет вид

                                      .

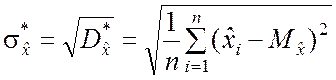Требуется выявить основные свойства .

1. Из вышеизложенного следует, что  является состоятельной и асимптотически эффективной оценкой .

2. Поскольку

                                            ,

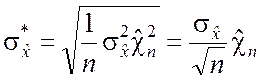то

                            ,

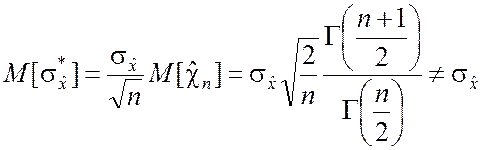где 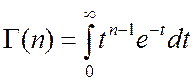 - гамма-функция (интеграл Эйлера 2 рода).

Полученное соотношение указывает на смещённость оценки среднего квадратического отклонения.

Если величину  исправить, умножив её на коэффициент

                                                ,

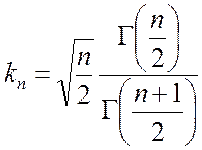то полученная в результате функция случайной выборки

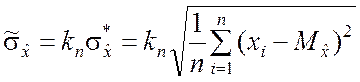                                             (5.2.5)

будет состоятельной, несмещённой и асимптотически эффективной оценкой среднего квадратического отклонения  случайной величины . В табл.5.1 приведены значения коэффициента k_n для некоторых n. Эти значения используются при вычислении оценки (5.2.5).

Таблица 5.1

Значения коэффициента k_n

n	2	3	4	5	6	9	12	18	24
kn	1,128	1,085	1,064	1,051	1,042	1,028	1,021	1,014	1,010

Из таблицы видно, что необходимость в исправлении оценки возникает лишь при малых объёмах выборки, так как с их увеличением коэффициент k_n достаточно быстро приближается к единице.

5.2.2. Оценивание дисперсии и среднего квадратического отклонения при неизвестном математическом ожидании

Для отыскания оценки дисперсии случайной величины необходимо знать её математическое ожидание . В случае, если данный параметр неизвестен, используют его оценку .

Рассмотрим функцию случайной выборки в виде статистической дисперсии