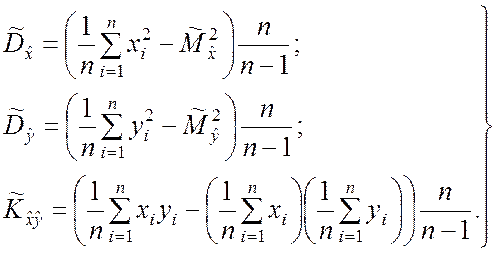Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 8

                                                                                    (5.3.4)

Очевидно, что оценка  коэффициента корреляции  найдётся по формуле

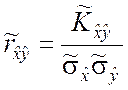                                                     .                        (5.3.5)

П р и м е р 5.9. Пусть  и  – координаты пробоины в мишени после выстрела (в сантиметрах). По мишени произведено 10 независимых выстрелов, результаты которых сведены в табл.5.4, где i – номер выстрела. Найти оценки числовых характеристик , , , , , системы случайных величин .

Таблица 5.4

Координаты пробоин в мишени

i	1	2	3	4	5	6	7	8	9	10
xi	3	1	2,5	1,5	4	3,5	2	2,5	1,5	1
yi	5	2	4	3,5	1,5	5,5	2,5	4,5	2	0

▼ По формулам (5.3.1) получим

                      ,   .

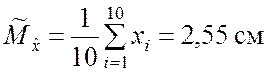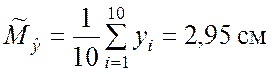Используя соотношения (5.3.4), имеем:

                           

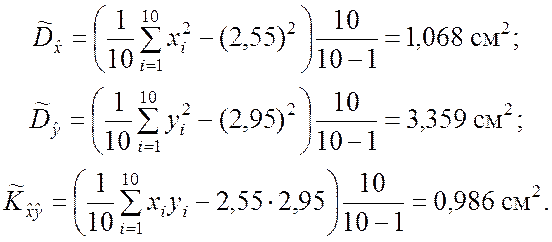
Наконец, используя табл.5.1, по формулам (5.2.13) и (5.3.5), получим:

                                            

                                      

                                         

▲

5.3.2. Многомерный случайный вектор

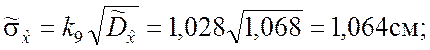
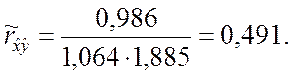
Аналогично решается задача оценивания числовых характеристик системы произвольного числа случайных величин.

Пусть имеется m случайных величин . Над системой произведено n независимых равноточных наблюдений, результаты которых оформлены в виде табл.5.5. Указанная таблица носит название простой статистической матрицы.

Таблица 5.5

Простая статистическая матрица

i	xij
	xi1	xi2	×××	xij	×××	xim
1	x11	x12	×××	x1j	×××	x1m
2	x21	x22	×××	x2j	×××	x2m
×××	×××	×××	×××	×××	×××	×××
i	xi1	xi2	×××	xij	×××	xim
×××	×××	×××	×××	×××	×××	×××
n	xn1	xn2	×××	xnj	×××	xnm

В табл.5.5 величины x_ij, ,  – это значения, принятые случайной величиной  в i-м опыте.

Требуется найти оценки числовых характеристик системы случайных величин, т.е. оценки математических ожиданий 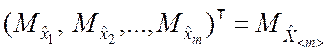 и элементов корреляционной матрицы

                             ,

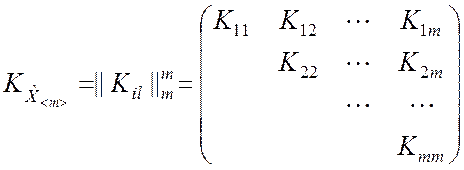где   ,   ,   .

Выведенные ранее формулы для вычисления состоятельных, несмещённых и эффективных (асимптотически эффективных) оценок числовых характеристик в общем случае системы m случайных величин приобретают следующий вид:

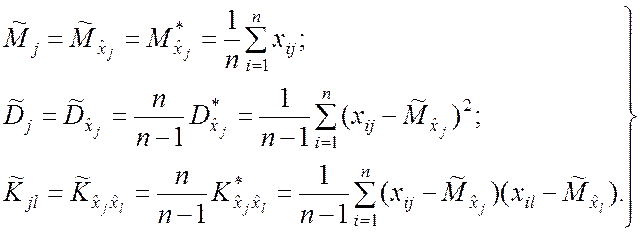                                                                        (5.3.6)

Для вычисления оценок (5.3.6) могут быть использованы формулы типа (5.3.4). Оценки средних квадратических отклонений:

                                         ,                        

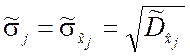Зная  и , нетрудно найти оценки элементов нормированной корреляционной матрицы по формулам

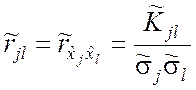                                       ,   .         (5.3.7)

5.3.3. Качество оценивания числовых характеристик случайных векторов

Основные вероятностные свойства m-мерного случайного вектора

                                            

описываются m-мерным вектором математических ожиданий его компонент

                   .

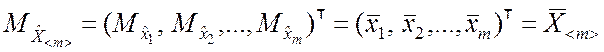и корреляционной матрицей m-го порядка

,

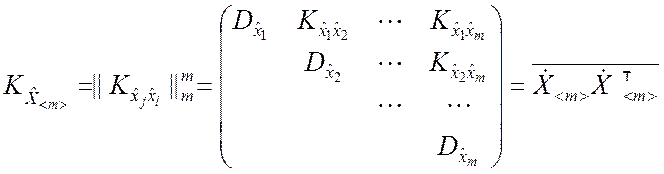т.е. всего  m + m²  числовыми характеристиками. Поскольку корреляционная матрица симметрична, то число различных её элементов равно 0,5(m + m²).  Таким образом, при оценивании числовых характеристик m-мерного случайного вектора  необходимо вычислить  0,5(m² + 3m) оценок, из которых m оценок 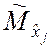 математических ожиданий , , такое же количество оценок  дисперсий ,  и 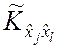 оценок  корреляционных моментов ,  .