Оценивание числовых характеристик и параметров распределения случайных объектов (Раздел 5 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 7

Потребный объём экспериментальных данных для оценивания дисперсии  с заданными точностью и надёжностью получим, если выразить n из уравнения (5.2.15):

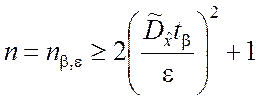                                            ,            (5.2.21)

Следует отметить, что n определяется, когда дисперсия ещё только подлежит оцениванию. Но значения и вероятностные характеристики оценки , входящей в выражение (5.2.21), зависят от объёма выборки. Поэтому объём n определяется методом последовательных приближений. В первом приближении задаются некоторым ориентировочным значением n₀, при котором вычисляется приближение  оценки . Затем оно уточняется в последующих циклах вычислений. Очевидно, что если n₀ превышает найденное по формуле (5.2.21) значение n, то принимается n = n₀. В данном случае оценка  =  уже удовлетворяет требованиям по точности и надёжности.

П р и м е р 5.8. В условиях примера 5.6:

1) найти приближённое значение числовых характеристик дисперсии случайной величины ;

2) построить 80-процентный доверительный интервал для дисперсии;

3) определить доверительную вероятность b для дисперсии, если максимальная с вероятностью b погрешность e_b = 0,02.

▼ 1. По формулам (5.2.10) получаем:

             ;    ;

                                       .

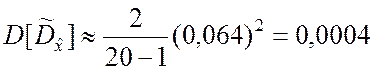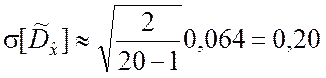2. Используем выражение (5.2.19):

                               .

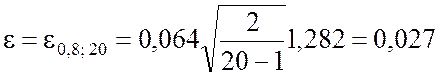Доверительный интервал для дисперсии в соответствии с (5.2.20):

           .

3. По формуле (5.2.18)

.

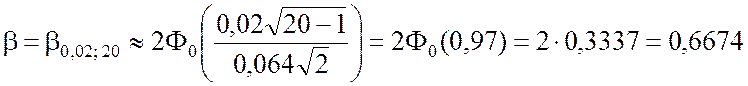Значение F₀(x) найдено в приложении 2.                                  

                                                                                                               ▲

5.3. Оценивание числовых характеристик и параметров распределения случайных векторов

5.3.1. Двумерный случайный вектор

В разделе 4 были рассмотрены методы оценивания закона распределения случайной величины во всех его возможных формах – ряда, функции и плотности распределения. Аналогичная задача возникает и при обработке экспериментальных данных в виде случайных векторов, т.е. систем стохастически связанных между собой случайных величин. Такие системы характеризуются многомерными законами распределения.

В данном параграфе более подробно остановимся на оценивании параметров распределения случайных векторов. При этом начнём с рассмотрения частного случая – двумерного вектора, т.е. системы двух случайных величин.

Над системой двух случайных величин  произведено n независимых равноточных наблюдений, в результате которых получена последовательность пар чисел ,  (табл.5.3), которые можно интерпретировать как координаты точек , , …,  плоскости.

Таблица 5.3

Двумерный массив экспериментальных данных

i	1	2	×××	i	×××	n
xi	x1	x2	×××	xi	×××	xn
yi	y1	y2	×××	yi	×××	yn

Требуется по результатам наблюдений определить состоятельные, несмещённые и эффективные (асимптотически эффективные) оценки числовых характеристик , , , ,  системы случайных величин . В данном случае  – корреляционный момент  и .

Задача определения точечных оценок параметров двумерного распределения решается так же, как и для одной случайной величины. При этом оценки координат ,  центра рассеяния системы  находятся по формулам

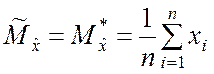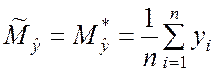,    ,                                                         (5.3.1)

а оценки элементов её корреляционной матрицы  определяются выражениями

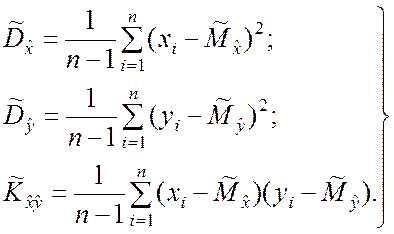                                        (5.3.2)

Если математические ожидания ,  известны, то элементы корреляционной матрицы определяются выборочными дисперсиями и корреляционным моментом (см. п.п. 5.2.1):

                                            

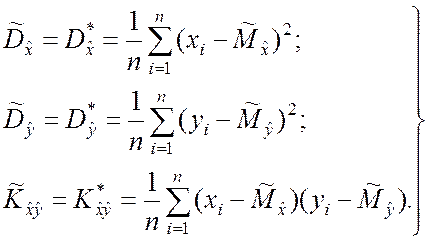
При вычислении оценок , ,  целесообразно воспользоваться известной связью между центральными и начальными моментами, которая имеет место и для их статистических аналогов

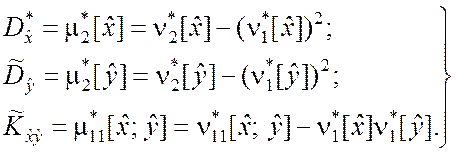                              (5.3.3)

С учётом (5.3.3) выражения (5.3.2) принимают вид, который обычно используется на практике: