Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных")

6. статистические гипотезы в ЗАдаЧАХ обработки экспериментальных данных

6.1. Понятие статистической гипотезы. Виды гипотез

Гипотезой принято называть предположение о некоторых свойствах изучаемых явлений. При обработке экспериментальных данных рассматриваются гипотезы о свойствах генеральной совокупности, например о виде закона распределения исследуемого признака, о параметрах закона распределения. Эти гипотезы проверяются путём обработки случайной выборки и в дальнейшем называются статистическими.

Наряду с принятой гипотезой рассматривают и противоречащую ей гипотезу, которая может быть принята в том случае, если первая не подтвердится. Для отличия эти гипотез друг от друга выдвинутую гипотезу принято называть нулевой или основной и обозначать символом H₀, а гипотезу, противоречащую нулевой, – конкурирующей или альтернативной и обозначать символом H₁.

Для краткости записи гипотез используют специальное обозначение. Пусть нулевая гипотеза состоит в предположении, что математические ожидания двух нормально распределённых случайных величин  и  равны, а конкурирующая гипотеза состоит в том, что они не равны. Эти гипотезы записываются следующим образом:

                                     ;    .

Гипотезы принято подразделять на простые и сложные. Простой называют гипотезу, содержащую только одно предположение, например . Сложной называют гипотезу, содержащую конечное или бесконечное число предположений. Например, гипотеза   состоит из бесконечного множества простых гипотез вида , где b_i – любое число, превосходящее 10.

Задачи проверки гипотез можно разделить на несколько классов, отличающихся друг от друга как по форме, так и по методом решения. Прежде всего, эти задачи делятся на параметрические, когда вид закона распределения известен, и непараметрические, когда закон распределения неизвестен. В свою очередь, каждый из данных классов содержит следующие подклассы.

1. Задачи согласия. Данные задачи сводятся к проверке согласия (соответствия) вида закона распределения или значений параметров распределения, выдвинутых в качестве предполагаемых, с законом распределения или параметрами закона распределения исследуемой случайной величины.

Формулировка данных задач имеет следующий вид. Нулевая гипотеза:

                                                    .

Конкурирующие гипотезы:

                       .

Здесь  и – символы сравниваемых случайных объектов. Так, если речь идёт о проверке согласия закона распределения, то , , где  – закон распределения исследуемой случайной величины;  – гипотетический закон распределения. Для данного случая получим:

                                      .

При проверке согласия параметров распределения альтернативные гипотезы могут выдвигаться в форме гипотез, содержащих бесчисленное множество предположений.

2. Задачи независимости. Эти задачи возникают в тех случаях, когда необходимо проверить, являются ли компоненты некоторого случайного вектора независимыми. Очевидно, что если компоненты вектора

                                            

независимы, то

                                          ,

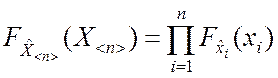где   – закон распределения случайного вектора ;  ,  – закон распределения i–го компонента вектора .

Поэтому задачу проверки гипотезы о независимости можно сформулировать следующим образом:

                                      ;

                                       .

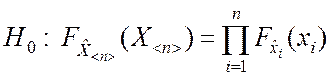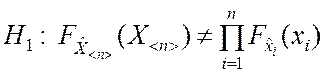3. Задачи проверки выборки. Данные задачи появляются в случае необходимости проверки того факта, что полученная выборка является простой, т.е. варианты выборки подчинены одному и тому же закону распределения.

Задачи такого типа формулируются в виде соотношений:

                                  ;

                                  .

6.2. Общий подход к проверке гипотез

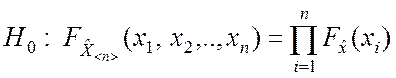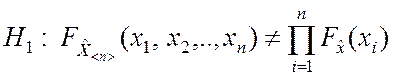Подход к решению задачи проверки гипотез рассмотрим на следующих двух примерах.

П р и м е р 6.1. На склад готовой продукции микросхемы одного типа поступают с двух заводов, выпускающих продукцию разного качества, и такими же партиями микросхемы отпускаются со склада потребителю. Качество продукции заводов характеризуется вероятностью p того, что случайным образом выбранная микросхема является бракованной. Для одного завода p = p₀, для другого p = p₁ (p₀ < p₁). Потребитель произвольно выбирает одну партию микросхем. Необходимо на основании результатов контроля решить, на каком заводе изготовлена выбранная партия микросхем.

▼ Введём нулевую гипотезу H₀, состоящую в том, что выбранная партия микросхем изготовлена на одном заводе (вероятность брака равна p₀), и конкурирующую гипотезу H₁ о том, что партия микросхем изготовлена на другом заводе (вероятность брака равна p₁).

Отберём из партии случайным образом n изделий. Обозначим число бракованных микросхем среди отобранных символом . Очевидно, что  – дискретная случайная величина, множество значений которой

                                               X_{n} = {0, 1, 2,..,n}.

Назовём решающим правилом или  критерием проверки гипотезы совокупность условий, при которых нулевая гипотеза принимается или отвергается.