Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 8

показывают, что при таком выборе критической области показатель согласованности  становится непригодным для статистической проверки гипотезы H₀, так как его мощность близка к нулю, а ошибки второго рода становятся практически достоверными. Очевидно, что для увеличения мощности показателя согласованности необходимо выбрать левостороннюю критическую область.

Если характер конкурирующей гипотезы неясен, то в качестве критической целесообразно выбирать двустороннюю симметричную область. Но следует отметить, что единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объёма выборки.

6.7. Проверка гипотез об аномальности результатов наблюдений

При обработке экспериментальных данных существенное значение имеет процесс предварительной обработки, одним из этапов которого является исключение результатов, содержащих грубые ошибки, т.е. аномальных результатов.

В любой выборке сомнительными являются, как правило, наибольший и наименьший элементы, которые и подлежат проверке. Обозначим через  и  наименьший и наибольший элементы случайной выборки , ,…, , а через x₁ и x_n – реализации этих элементов в данном эксперименте.

Предположим, что сомнительным является наибольший элемент x_n случайной выборки. При этом будем полагать, что наблюдаемая величина  подчинена нормальному закону распределения с известными числовыми характеристиками  и . Уровень значимости примем равным некоторой достаточно малой вероятности a. Для выборки, состоящей из одного элемента x, можно утверждать, что он является следствием грубой ошибки, если

                                                             (6.7.1)

или

                                                  .                               

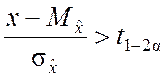Следовательно, при n = 1 в качестве показателя согласованности гипотезы целесообразно использовать случайную величину

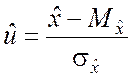                                                     ,                       (6.7.2)

а критическую границу определять на основе выражения

                                                       u_a = t_1–2a.                          (6.7.3)

Однако при проверке аномальности крайнего элемента случайной выборки объёма n > 1 использование показателя согласованности вида (6.7.2) может привести к грубым ошибкам. Покажем это на примере.

П р и м е р 6.3. Пусть n = 1 и a = 0,05.

▼ В приложении 4 находим

u_a = t_1–2a = t_0,9 = 1,64.                                  (6.7.4)

Подставив найденное значение u_a в формулу (6.7.1), получим

                                             .               (6.7.5)

Таким образом, при одном испытании будем констатировать факт грубой ошибки, если наблюдаемое значение случайной величины удовлетворяет неравенству (6.7.5).

Увеличим теперь число испытаний до 20 и найдём вероятность того, что наибольший член  выборки превзойдёт величину x_a:

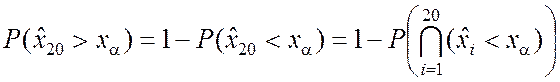                      .                                                         (6.7.6)

Предполагая, что испытания независимы, и учитывая, что

                            ,   ,        

из выражения (6.7.6) получим

                          .

Таким образом, при использовании критической границы, определяемой выражением (6.7.4), 65% нормальных наибольших элементов выборки следует признать аномальными. Иначе, вероятность ошибки первого рода при 20 испытаниях увеличится до 0,65.

▲

С целью устранения указанного недостатка необходимо по мере увеличения объёма выборки сдвигать критическую границу вправо относительно значения u_a, определяемого равенством (6.7.4).

Для построения критической области, удовлетворяющей указанному требованию, рассмотрим функцию распределения . Примем во внимание то обстоятельство, что для наступления события ( < x) необходимо, чтобы все элементы выборки были меньше x: