Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

-  методы, опирающиеся на оценки потерь от неправильного решения;

-  методы, опирающиеся на оценки вероятностей ошибок при принятии решений.

Наибольшее практическое распространение получили методы второй группы, так как их применение требует минимальной априорной информации при проверке гипотез, однако, достоверность принятия решений с помощью данных методов ниже, чем для методов первой группы.

6.5. Проверка гипотез как задача принятия решений

Чтобы формализовать задачу проверки статистических гипотез в виде задачи принятия решения, опишем эту задачу в терминах теории статистических решений.

В качестве объекта наблюдения здесь выступает гипотеза H. Будем полагать, что два возможных варианта данной гипотезы – нулевая H₀ и конкурирующая H₁ представляют собой простые гипотезы.

В качестве статистической характеристики гипотезы используется показатель согласованности , являющийся некоторой функцией результатов наблюдения.

Множество решений включает в себя: решение , состоящее в принятии гипотезы H₀, и решение , состоящее в отклонении гипотезы H₀ (т.е. принятии гипотезы H₁).

Объём априорной информации в процессе принятия гипотез может быть различен. Так, при минимальной неопределённости она включает в себя (см. § 2.3):

-  вероятности наступления гипотез H₀ и H₁, данные вероятности запишем как  и ;

-  законы распределения показателя согласованности  при условии справедливости нулевой и конкурирующей гипотез, т.е. условные плотности распределения  и ;

-  функцию потерь p, задаваемую в виде матрицы потерь:

                                                  .

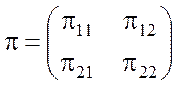Решающее правило для данного случая состоит в разделении множества возможных значений показателя согласованности  на два подмножества D и Q. Попадание наблюдаемого значения в первое из них означает принятие решения о справедливости гипотезы H₀, а второе - принятие решения об отклонении H₀. Таким образом, решающее правило определяет выбор критической границы или границ, если их несколько, и, таким образом задаёт критическую область Q.

Решающее правило может быть сформулировано на основе принципов принятия статистических решений. При проверке гипотез используется четыре вида правил, причём применение того или иного вида зависит от полноты априорных данных.

Если задача проверки гипотез сформулирована как задача выбора решений и матрица потерь p определена, то оптимальное решение может быть получено на основе байесовского или минимаксного правила.

Если функция потерь p не определена, то для однозначного выбора решения при проверке гипотез можно использовать два подхода. Применительно к задачам с известным априорным распределением гипотез наиболее полной характеристикой степени соответствия каждой из них результатам произведённого испытания является апостериорная вероятность этой гипотезы. При этом истинной считается апостериорная вероятность. Указанное правило называется правилом апостериорной вероятности.

При отсутствии данных об априорном распределении гипотез единственной характеристикой степени соответствия той или иной гипотезы результатам наблюдения является функция правдоподобия.

Поэтому в таких случаях выбор решений производится на основе правила максимума правдоподобия, в соответствии с которым истинной считается гипотеза с наибольшим значением функции правдоподобия.

6.6. Проверка гипотез классическим методом

Применение рассмотренных выше методов, как уже отмечалось, связано с использованием априорной информации, которая далеко не всегда имеется в распоряжении исследователя при обработке экспериментальных данных. В связи с этим на практике наибольшее распространение получили методы проверки гипотез, опирающиеся при назначении критических границ только на информацию о вероятностях ошибок первого и второго рода.