Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

                                             ;                (6.3.1)

-  в виде зависимости от гипотетической вероятности p и частоты p^*, полученной в результате проведения эксперимента:

                                                   .                               

При проверке гипотезы о равенстве математических ожиданий двух независимых случайных величин  и  показатель согласованности может выбираться в виде различного рода зависимостей от начальных и центральных моментов первого и второго порядков от случайных величин  и :

                                   .               

Применяются также и другие виды зависимостей. Однако, несмотря на такое разнообразие, в любом случае показатель согласованности должен удовлетворять ряду требований. Поскольку это величина случайная, то и требования формулируются применительно к закону распределения показателя согласованности. Состоят они в следующем.

1. Показатель согласованности должен определяться нулевой и конкурирующей гипотезами, а также  условиями проведения эксперимента. Так, в показателе согласованности, определяемом выражением (6.3.1), эта зависимость представлена наличием как гипотетической, так и статистической функций распределения в качестве аргументов функции f₁.

2. Показатель согласованности должен представлять собой случайную величину, точное или приближённое распределение которой известно. В настоящее время наиболее распространён выбор показателей согласованности, распределённых по нормальному закону, законам хи-квадрат,  Стьюдента,  Фишера. Причём показатели согласованности с различными законами распределения обозначаются разными символами. Так, показатели, распределённые по нормальному закону, обозначают через  u  или z, по закону хи-квадрат – через c², по закону Стьюдента – через  t, по закону Фишера – через F.

3. Закон распределения показателя согласованности должен быть инвариантен к виду закона распределения исследуемой случайной величины. Именно данное обстоятельство и определило широкое распространение показателей согласованности, имеющих указанные выше законы распределения.

4. Для построения закона распределения показателя согласованности должен  быть востребован минимум априорных сведений, так как возможность получения достоверных сведений до опыта существенно ограничена.

5. Закон распределения показателя согласованности должен быть критичен по отношению к проверяемой гипотезе. Указанное требование означает, что условные плотности распределения  и  должны существенно отличаться друг от друга.

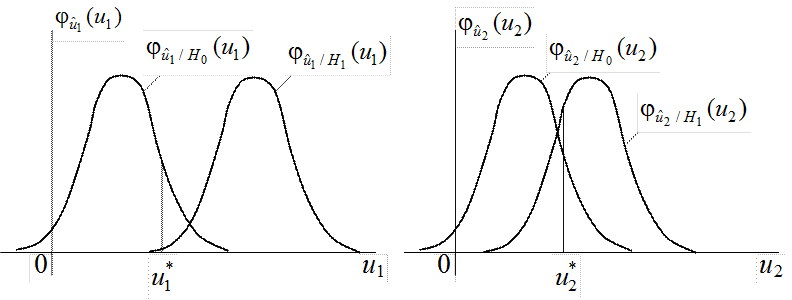
Рис.6.1. Условные плотности распределения показателей согласованности

На рис.6.1 изображены кривые условных плотностей распределения двух различных показателей согласованности  и  при нулевой и конкурирующей гипотезах. Из сравнения кривых видно, что применение показателя  предпочтительнее, так как он обеспечивает более высокую степень уверенности различения гипотез H₀ и H₁, чем показатель . Действительно, при одном и том же значении , т.е. при наступлении одного и того же события , вероятность отнесения его к нулевой гипотезе значительно выше, когда используется показатель .

В заключение следует отметить, что для проверки гипотезы по данным выборки вычисляют частные значения входящих в показатель согласованности величин и, таким образом, получают частное значение показателя согласованности гипотезы. Это значение, вычисленное по данным выборки, в дальнейшем будем называть наблюдаемым значением показателя согласованности  и обозначать через u.

6.4. Методы задания критической области