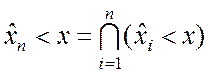Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 9

                                               .                  (6.7.7)

Далее учитываем, что

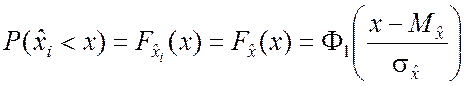                             .              (6.7.8)

К правой части выражения (6.7.7) применяем теорему умножения вероятностей независимых событий ( < x),  и принимаем во внимание (6.7.8). В результате получаем

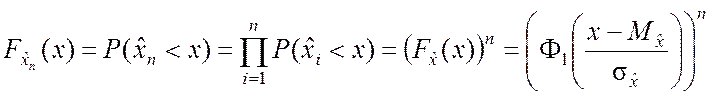     .       (6.7.9)

Границу u_a критической области, отвечающей уровню значимости a, можно найти как квантиль случайной величины  при аргументе 1–a. Зависимость между u_a и a определяется равенствами:

                                                 ;                              

                                                  .                   (6.7.10)

Подставляем x = u_a в формулу (6.7.9) и на основании равенства (6.7.10) получим уравнение

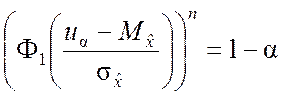                                          .           (6.7.11)

Решаем (6.7.11) относительно  u_a  и находим

                                            .            (6.7.12)

Так как вероятность a обычно мала, то

                                                 

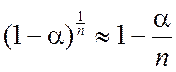
и, следовательно,

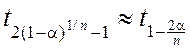                                                 .                 (6.7.13)

Подставляя соотношение (6.7.13) в (6.7.12), получим

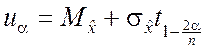                                                .                (6.7.14)

Выражение (6.7.12) и применяется для определения критической границы в случае, если  n > 1.

Порядок проверки гипотезы об аномальном значении наибольшего элемента выборки состоит в следующем.

1. Элемент, относительно которого выдвигается гипотеза, исключается из выборки, т.е. её объём уменьшается на единицу.

2. Назначается уровень значимости a и по приложению 4 определяется значение .

3. По формуле (6.7.14) определяется критическая граница. При отсутствии априорных значений  и  в данной формуле используются оценки  и . При их вычислении предполагаемый аномальный результат из выборки исключается.

4. Наблюдаемое значение показателя согласованности гипотезы определяется по формуле

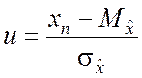                                                    .                     (6.7.15)

5. Проверяется условие u > u_a. Если оно выполняется, то наибольший элемент выборки, по отношению к которому выдвигалось предположение о наличии грубой ошибки, отбрасывается. При u £ u_a этот элемент сохраняется в выборке, поскольку данные эксперимента не подтверждают гипотезы о наличии грубой ошибки. Для подтверждения полученного вывода необходимо повторить проверку по пунктам 1–5, но с включением сомнительного элемента в выборку.

При рассмотрении в качестве аномального наименьшего элемента  случайной выборки, порядок проверки гипотезы сохраняется, но в качестве показателя согласованности последней используется случайная величина

                                                    .                                

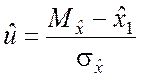При этом проверяемый элемент отбрасывается, если u > u_a, и сохраняется в противном случае.

П р и м е р 6.4. С помощью радиодальномера производятся 20 измерений дальности  до объекта. Точность радиодальномера характеризуется среднеквадратическим отклонением  = 50 м. Имеются ли основания полагать, что наибольшее отклонение

                                                ,

зафиксированное в данной серии наблюдений, содержит грубую ошибку? Уровень значимости критерия проверки гипотезы принять равным 0,05.

▼ По условию задачи n = 20, a = 0,05. В соответствии с выражением (6.7.15) значение показателя согласованности

                                          .                      

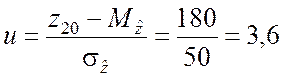Границу критической области находим в приложении 4:

                                      .

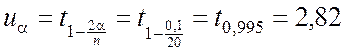Так как u > u_a, то наибольшее отклонение содержит грубую ошибку и его следует из дальнейшего рассмотрения исключить.

▲