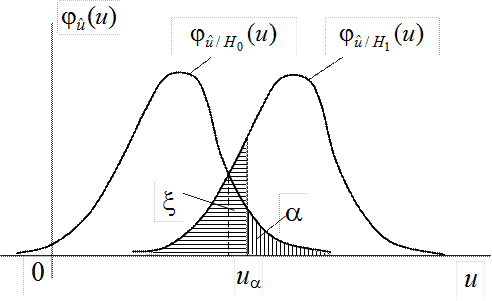
Рис.6.4. Взаимозависимость ошибок первого и второго рода
Следует напомнить, что вероятность ошибки первого рода
равняется вероятности a
попадания показателя ![]() в критическую область. Чем
меньше уровень значимости a,
тем реже будет допускаться ошибка первого рода, а, следовательно, отвергаться
правильная нулевая гипотеза H0.
Однако было бы неверно на основании этого делать вывод о том, что значение
вероятности a должен быть
выбрано как можно меньшим.
в критическую область. Чем
меньше уровень значимости a,
тем реже будет допускаться ошибка первого рода, а, следовательно, отвергаться
правильная нулевая гипотеза H0.
Однако было бы неверно на основании этого делать вывод о том, что значение
вероятности a должен быть
выбрано как можно меньшим.
Из рис. 6.4 видно, чем меньше a, тем больше вероятность
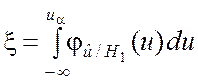 (6.6.2)
(6.6.2)
ошибки второго рода.
Указанная взаимосвязь ошибок первого и второго рода позволяет
сделать следующий важный вывод: для уменьшения вероятности ошибки при принятии
гипотезы критическую границу необходимо выбирать таким образом, чтобы сумма
вероятностей ошибок первого и второго рода была минимальной (см. п.п.2.3.3).
Если показатель согласованности подчинён нормальному закону, то минимум суммы
вероятностей ошибок первого и второго рода достигается при выборе критической
границы в абсциссе точки пересечения кривых распределения ![]() и
и ![]() . На
рис.6.4. указанное деление показано пунктиром.
. На
рис.6.4. указанное деление показано пунктиром.
Вместе с тем следует заметить, что не во всех случаях подход к выбору ua с учётом минимума суммы вероятностей ошибок первого и второго рода целесообразен. На практике выбор целесообразной величины a зависит от «тяжести» последствий ошибок первого и второго рода для каждой конкретной задачи. Например, если ошибка первого рода повлечёт большие потери, а второго рода – малые, то целесообразно принять возможно меньшее a. Вернёмся к примеру 6.1 и рассмотрим, какую величину уровня значимости критерия проверки целесообразно выбрать с точки зрения потребителя микросхем. Заметим, что в задачах подобного типа вероятность приёма бракованной партии изделий (в нашем примере – микросхем), т.е. вероятность ошибки первого рода, принято называть риском потребителя, а вероятность признать бракованной партию качественных изделий (вероятность ошибки второго рода) – риском производителя. С точки зрения потребителя желательно уменьшать вероятность приёма бракованной партии микросхем, т.е. уменьшать вероятность ошибки первого рода, в связи с чем величину a целесообразно выбирать возможно меньшей.
Поскольку вероятность ошибки второго рода также играет важную роль при выборе критической области, то критерий проверки принято характеризовать так называемой мощностью показателя согласованности.
Мощностью g показателя
согласованности называют вероятность попадания показателя
согласованности ![]() в критическую область при
условии, что справедлива конкурирующая гипотеза.
в критическую область при
условии, что справедлива конкурирующая гипотеза.
На основе определения можно записать
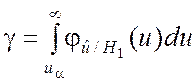 . (6.6.3)
. (6.6.3)
С учётом выражения (6.6.2) равенство (6.6.3) примет вид
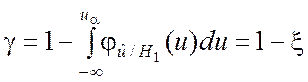 .
.
Таким образом, мощность показателя согласованности – вероятность того, что не будет допущена ошибка второго рода. Поэтому для уменьшения ошибки второго рода критическую область необходимо строить так, чтобы мощность показателя согласованности при заданном уровне значимости была максимальной.
Мощность показателя согласованности позволяет обоснованно подойти
к выбору односторонних критических областей. Предположим, что в качестве
критической выбрана правосторонняя область (рис.6.4), но кривая условной
плотности распределения для конкурирующей гипотезы ![]() смещена
относительно кривой
смещена
относительно кривой ![]() влево (рис.6.5).
влево (рис.6.5).
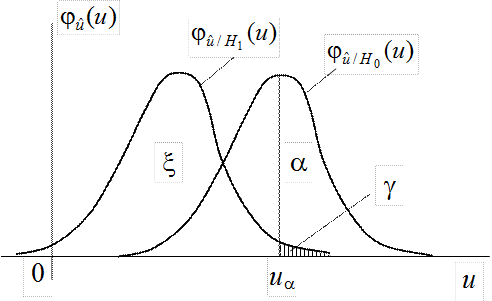
Рис.6.5. Условные распределения показателя согласованности гипотез
Найденные в этих условиях вероятности
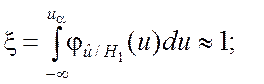
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.