Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

Как отмечалось выше, проверка гипотез требует задания решающего правила, т.е. метода разбиения множества U возможных значений показателя согласованности  на два подмножества: подмножество U₀, при попадании в которое наблюдаемого значения u  показателя  нулевая гипотеза принимается, и подмножество U₁, при попадании в которое наблюдаемого значения u  нулевая гипотеза отвергается. В дальнейшем область, соответствующую U₀, будем называть областью допустимых значений (областью принятия гипотезы H₀) и обозначать символом D, а область, соответствующую подмножеству U₁ – критической областью показателя  и обозначать символом Q.

Поскольку  – одномерная случайная величина, то все её возможные значения принадлежат некоторому интервалу. Поэтому области Q и D являются интервалами, следовательно, существуют разделяющие их точки. Они называются критическими точками (границами). Задание критической области и сводится к заданию критических точек.

Сущность задания критических точек состоит в следующем. Рассмотрим события:

 – верна гипотеза H₀;

 – верна гипотеза H₁;

 – наблюдаемое значение u  показателя согласованности  попало в область D;

 – наблюдаемое значение u  попало в область Q.

Тогда в процессе принятия решения возможен один из следующих исходов:

 – верна гипотеза H₀ и принято решение о её справедливости;

– верна гипотеза H₀, а принято решение о справедливости гипотезы H₁;

– верна гипотеза H₁, а принято решение о справедливости гипотезы H₀;

 – верна гипотеза H₁ и принято решение о её справедливости.

Очевидно, что исходы  и  являются ошибочными, первому из них соответствует ошибка первого рода, а второму – ошибка второго рода.

Таким образом, под ошибкой первого рода понимается принятие решения об отклонении нулевой гипотезы в случае, если в действительности она является правильной, а под ошибкой второго рода – решение о принятии нулевой гипотезы, если в действительности она не верна.

Поскольку рассмотренные события являются случайными, то им могут быть поставлены в соответствие вероятности наступления данных событий, а именно:

p₁₁ – вероятность наступления события  ;

p₁₂ – вероятность наступления события  ;

p₂₁ – вероятность наступления события ;

p₂₂ – вероятность наступления события .

Значения  p₁₁, p₁₂, p₂₁, p₂₂  можно вычислить как вероятности попадания случайной величины  в области D и Q следующим образом.

Пусть законы распределения показателя согласованности  при условии, что справедлива нулевая или конкурирующая гипотеза заданы в форме плотности распределения  и , а границей данных областей является точка . Предположим, что взаимное расположение кривых распределения  и , а также областей D и Q имеет вид, изображённый на рис.6.2.

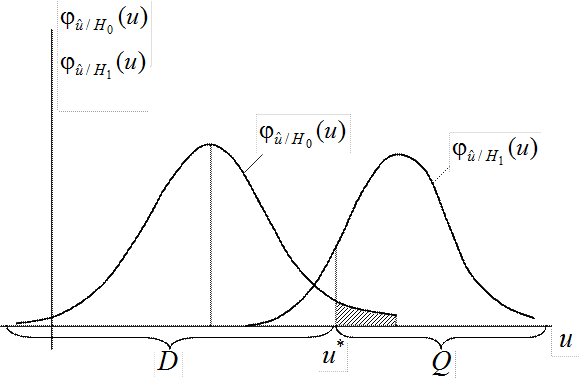
Рис.6.2. Кривые распределения показателя согласованности при различных гипотезах

В этом случае вероятности p₁₁, p₁₂, p₂₁, p₂₂ определяются следующими соотношениями:

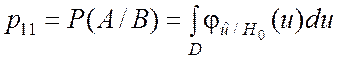                                      ;         (6.4.1)

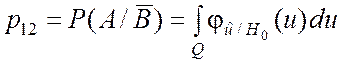                                      ;        (6.4.2)

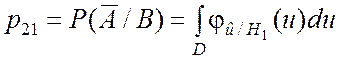                                      ;         (6.4.3)

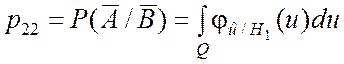                                      .        (6.4.4)

Из выражений (6.4.1) – (6.4.4) следует, что значения p₁₁, p₁₂, p₂₁, p₂₂ зависят от размеров и расположения области D допустимых значений и критической области Q. Поэтому, предъявляя соответствующие требования к вероятностям p₁₁, p₁₂, p₂₁, p₂₂, можно определить расположение и размеры данных областей, т.е. критические границы.

Так как проверка гипотезы связана с принятием решения о справедливости или несправедливости выдвинутой гипотезы, то при нахождении областей D и Q целесообразно опираться на результаты теории статистических решений (см. § 2.3). Практическое применение данных результатов зависит от объёма априорной информации, которая может быть использована при проверке гипотез. В связи с этим методы задания критической области принято делить на две группы [5]: