Статистические гипотезы в задачах обработки экспериментальных данных (Раздел 6 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

Сущность данных методов состоит в задании вероятности p₁₂ ошибки первого рода. Зная эту величину и зависимость, связывающую вероятность p₁₂ с показателем согласованности , можно определить границы и расположение критической области Q.

В связи с тем, что вероятность p₁₂ ошибки первого рода играет в данных методах ведущую роль, она имеет специальное название – уровень значимости критерия проверки гипотезы и специальное обозначение . Таким образом, в соответствии с выражением (6.4.2)

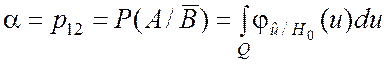                                   .     (6.6.1)

Если известны  и a, то выражение (6.6.1) позволяет определить критические границы, т.е. границы области Q. Данные границы в дальнейшем будем обозначать символами u_a1, u_a2,…, если область Q состоит из нескольких подобластей, или символом u_a, если она представляет собой одну область, т.е. возможные значения показателя согласованности  делятся границей u_a на две полупрямые.

При конкретном выборе критических границ u_a необходимо учитывать два дополнительных обстоятельства, а именно:

-  соотношение между условными законами распределения показателя согласованности , соответствующими нулевой и альтернативной гипотезам;

-  взаимозависимость ошибок первого и второго рода.

Поясним эти обстоятельства более подробно. Соотношение между условными законами распределения показателя согласованности , соответствующими нулевой и конкурирующей гипотезам, выражается в виде взаимного расположения их кривых распределения на оси абсцисс. Особенности характеристики , а также нулевой и конкурирующей гипотез приводят к тому, что кривые распределения ,  могут располагаться друг относительно друга тремя различными способами:

-  известно, что кривая распределения  сдвинута относительно  вправо (рис.6.3,а);

-  известно, что кривая распределения  сдвинута относительно  влево (рис.6.3,б);

-  сдвиг кривой распределения  неизвестен, т.е. она может быть сдвинута относительно  как вправо, так и влево (рис.6.3,в).

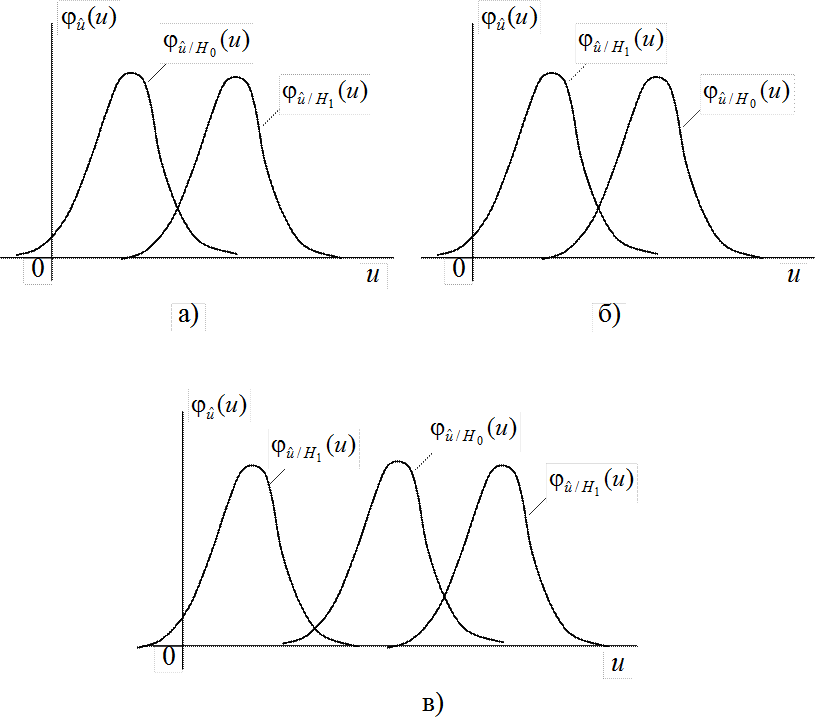
Рис.6.3.Варианты расположения  условных  законов  распределения  показателя согласованности

Очевидно, что вид критической области для каждого способа должен быть различен, а именно в первом случае должна быть выбрана правосторонняя критическая область, во втором – левосторонняя и в третьем – двусторонняя. Правосторонней называют критическую область, определяемую неравенством u > u_a, левосторонней – неравенством u < u_a, двусторонней – неравенствами  u < u_a1,  u > u_a2,  где  u_a2 > u_a1.

При отыскании критической области достаточно найти критические точки. Методика их отыскания состоит в следующем. Задаются уровнем значимости a и ищут критическую точку u_a, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность попадания показателя согласованности  в критическую область была равна принятому уровню значимости.

На основании (6.6.1) для правосторонней критической области это условие имеет вид

                                      ,                  

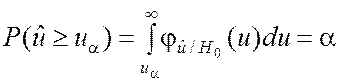для левосторонней

                                      ,                  

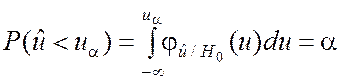для двусторонней

           .                                                              

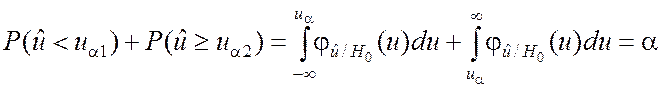В последнем случае чаще всего выбирают симметрично расположенные критические точки:

                                       .                    

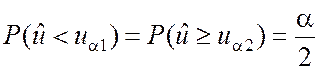Критические точки, удовлетворяющие приведённым выше условиям, находят по соответствующим таблицам (см., например, приложения 5 и 6).

Из вышеизложенного следует, что при выборе критических областей необходимо учитывать не только свойства нулевой, но и свойства конкурирующей гипотезы.

Для пояснения взаимозависимости ошибок первого и второго рода рассмотрим условные плотности ,  и правостороннюю критическую область с критической границей u_a, см. рис.6.4.