Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 9

3*Р₁ =3 (6, 17) = (8, 20).

Приклад 3

Нехай є ЕК з рівнянням: , a=1, b=1, p=23

Перевірити, чи належать слідуючи точки ЕК:

(1, 7), (1, 16).

Розв’язок задачі:

, точка (1,7) не належить ЕК;

, точка (1,16) належить ЕК;

Приклад 4

Знайти порядок базової точки (17, 20). Якщо рівняння еліптичної кривої має вигляд

Розв’язок задачі:

Для визначення порядку точки (17, 20) на еліптичній кривій  знайдемо таке значення d, щоб d*(17, 20) (mod 23) = 0

Для цього підставимо в останнє порівняння d = 1, 2, 3, … k, та визначимо значення скалярного добутку.

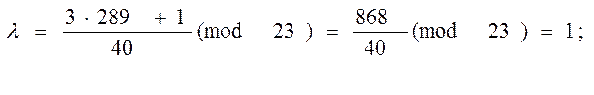
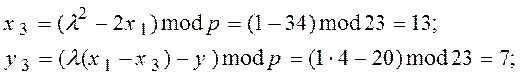
При d = 2 маємо

При d = 3

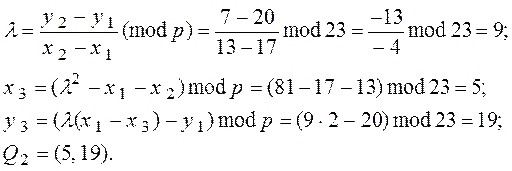
При d = 4 маємо

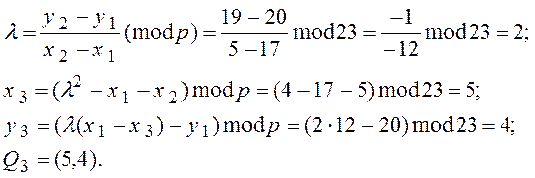
При d = 5

P₁ + Q₃ =Q₄

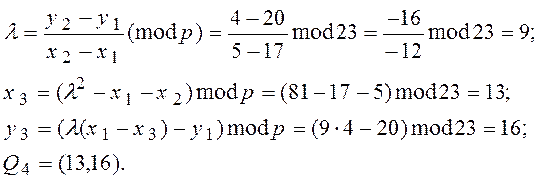
При d = 5

P₁ + Q₄=Q₅

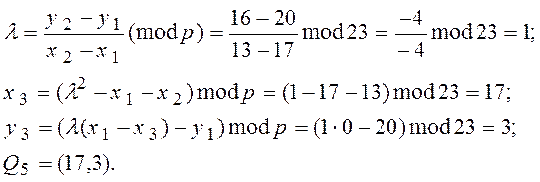
При d = 6

P₁ + Q₅=Q₆

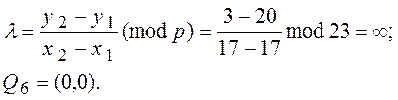
Таким чином порядок n точки G = (17, 25) на еліптичній кривій дорівнює 7.

Приклад 5

Побудувати , m=4, ,

Розв’язок задачі:

Поле - може бути задано 16 поліномами не вище третього ступеня, наприклад, поліномами над полем GF (2).

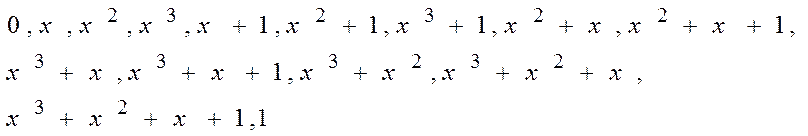
Елементи поля можуть бути задані в двійковому вигляді, тоді, наприклад,

x³+ x²+1Þ1101

x⁷+1Þ1101

Операція множення елементів поля виконується в полі GF(P).

Наприклад

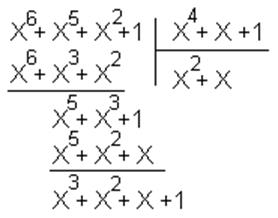
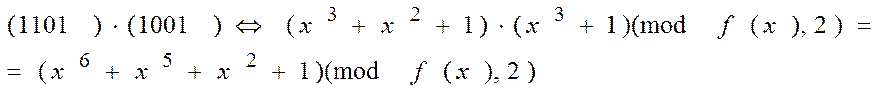
Приведемо цей поліном за модулем f(x) = x⁴+ x+1. У результаті маємо

Елементи поля можна одержати як aⁱ = a^j (mod f(x),2), j=

В таблиці наведені елементи aⁱ для f=

Таким чином (x³+ x²+1)(x³+ 1)(mod (x⁴+ x+1),2) = x³+ x²+x +1Þ1111

Приклад 5

 , m=4, ,

Знайти , якщо  .

Розв’язок задачі:

Знайдемо :

;

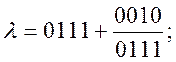
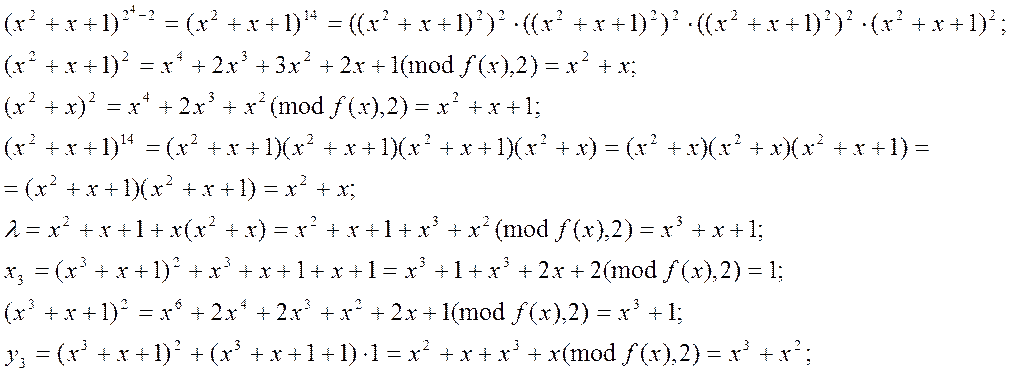
Знайдемо :

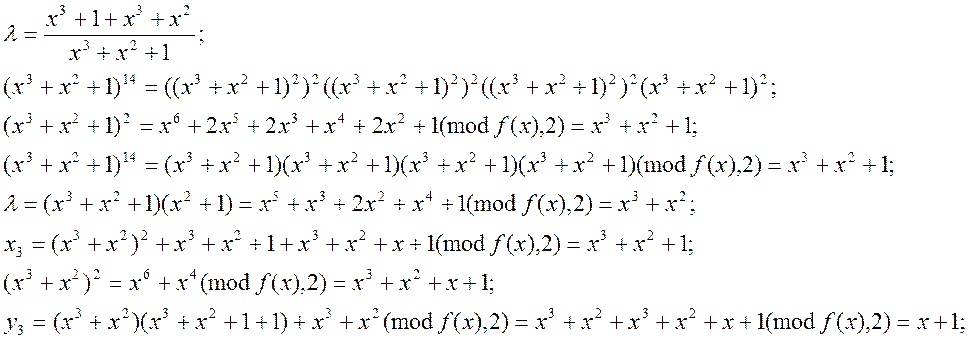     Таким чином

.

3.4 Задачі для самостійного розв’язку

1. Нехай є ЕК з рівнянням: , a=1, b=1, p=23

Перевірити, чи належать точки, наведені в таблиці еліптичній кривій:

N	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	(3, 10)	(3, 13)	(4, 0)	(5, 4)	(5, 19)	(6, 4)	(6, 19)	(7, 11)	(7, 12)	(9, 7)	(9, 16)	(17, 3)	(17, 20)	(18, 20)	(19, 5)	(13, 16)

Якщо n= k (mod 17), k – номер в журналі.

Якщо k=17, то k=k+1.

2. Знайти  (з попередньої задачі).

3. Знайти , якщо  (з попередньої задачі).

4. Знайти   і , якщо , якщо еліптична крива має вигляд ,

	1	2	3	4	5	6	7	8

k – номер за списком, якщо k=8, то      

3.5 Контрольні запитання:

1.  Дати визначення базової точки.

2.  Запишіть формулу складання точок еліптичної кривої над простим полем.

3.  Запишіть формулу подвоєння точок еліптичної кривої над простим полем.

4.  Запишіть формулу складання точок еліптичної кривої над розширеним полем.

5.  Запишіть формулу подвоєння точок еліптичної кривої над розширеним полем.

6.  Яким вимогам задовольняє примітивний поліном f(x)?

7.  Скільки елементів в полі GF(2^m), якщо m = 4, 9, 81, 160?

8.  Скільки елементів в полі GF(P), якщо P = 17, 31, 47, 89, 107, 257?

9.  Запишіть елементи поля GF(7).

10.  Запишіть елементи поля GF(2³).

11.  Поясніть рівняння еліптичної кривої над простим полем GF(P).

12.  Поясніть рівняння еліптичної кривої над розширеним полем GF(2^m).

ПРАКТИЧНЕ ЗАНЯТТЯ 4

РОЗРОБКА ТА АНАЛІЗ ВЛАСТИВОСТЕЙ АЛГОРИТМІВ ФОРМУВАННЯ ПСЕВДОВИПАДКОВИХ ТА ВИПАДКОВИХ ПОСЛІДОВНОСТЕЙ

4.1. МЕТА ЗАНЯТТЯ – освоєння методики розробки алгоритмів та на їх основі програмних та програмно – апаратних засобів формування псевдовипадкових послідовностей, виконання аналізу властивостей послідовностей згідно діючих методик та прийнятих критеріїв [1, 6, 12-14].

4.2. ОСНОВНІ ВІДОМОСТІ З ТЕОРІЇ

4.2.1. Основні вимоги до засобів формування випадкових та псевдовипадкових послідовностей.