Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 3

У (1.1) С_і є криптозахищена інформація М_і з використанням ключа K_j^пр, прямого перетворення та параметрів P_n . В (1.2) K_j^зв є ключ зворотного перетворення захищеної інформації С_і. В окремому випадку F_пр та F_зв є перетвореннями типу зашифрування та розшифрування. Тому (1.1) та (1.2) можна представити як:

С_і = F_з(M_i, K_j^з, P_n )                                                        (1.3)

M_і = F_р(C_i, K_j^р, P_n )                                                       (1.4)

У (1.3) С_і є криптограма (зашифроване повідомлення), М_і – відкрита інформація (з доступним смисловим змістом).

Криптоперетворення, в яких

K_j^пр = K_j^зв ,   K_j^з =K_j^р ,                                                    (1.5)

або один з ключів (наприклад K_j^зв) може бути визначений при відомому K_j^зв зі складністю не вище ніж поліноміальна, будемо називати симетричними криптоперетвореннями. Криптограми, в яких названі умови не виконуються будемо називати несиметричними (асиметричними).

Для класифікації та характеристики криптоперетворень можна використати різні показники і критерії. Найбільш переважним є використання таких характеристик:

Nk - об'єм ключів.

Н(k) - ентропія джерела ключів:

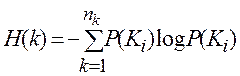                                               (1.6)

-   імовірність появи K_i  ключа в системі.

tб - безпечний час.

lo- відстань єдності КП.

Значення tб є математичне очікування часу розкриття КП з використанням конкретного методу. Найбільш простий   метод підбору або грубої сили, тоді якщо треба перебрати  N_в  варіантів то

,                                                                   (1.7)

де

- імовірність, з якою необхідно здійснити криптоаналіз.

g - продуктивність криптографічної системи (КАС),  зміна кількості можливих переборів в сек.

 сек/рік.

У граничному випадку Nв = Nк, де Nк  – число дозволених N ключів.

Система Вернама (безумовно стійкі криптоперетворення)

У системі здійснюється потокове шифрування, тобто символи криптограми в шифраторі зашифровуються за правилом:

                                                       mod m                   (1.8)

Мi  –  i-тий символ інформації, , а К_і  - і-й символ ключа, m – основа алфавіту.

Результат -  С_і – зашифрований текст (криптограма).

Відмітною особливістю в системі Вернама є те, що символи ключа Кi повинні породжуватись випадковим процесом. У такій системі довжина ключа повинна бути не менше за довжину повідомлення.

Розшифрування здійснюється за правилом

,                                                  (1.9)

де: Сi – символи криптограми, Кi – символи ключа, m – основа алфавіту.

Аналіз (1.8) і (1.9) показує, що для зашифрування і розшифрування треба використати одну і ту ж випадкову послідовність (ключ).

Відстань єдності для безумовно стійких (БС) і обчислювально стійких(ОС) КП:

Задача оцінки відстані єдності. Криптоаналітик послідовно перехоплює криптограми С₁,…С_n і вирішує задачу визначення смислового змісту М_i повідомлення, що передається  і, як найбільш важливу, задачу визначення ключів Кj.

Очевидно, що його успіх в рішенні задач залежить від об'єму криптограм, які він отримав, при цьому КРА знаходиться в невизначеності .

Найкращий випадок для криптоаналітика, якщо .

Шеннон ввів функцію ненадійності криптоперетворення:

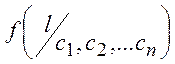                                                          (1.10)

l- загальний об'єм символів криптограми, який необхідно перехопити для рішення задачі криптоаналізу. Очевидно, є значення l₀ при якому,. З іншого боку він передбачив, що для лінійних шифрів можна скласти і вирішити систему лінійних рівнянь і вона буде мати одне рішення, при умові, що є l₀ незалежних коефіцієнтів для підстановки в цю систему. При цьому рішення самої задачі може бути дуже складним, але воно буде єдине. Для деякого класу лінійних (групових) шифрів, в яких використовуються природні мови (російська, англійська, С++, графіка) він отримав рівняння зв'язку  з ентропією джерела ключа Н(К), довжиною  l та  d -  надмірність мови.

                                                     (1.11)