Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 20

x₃ = 210;  НОД (191,221) = 1

x₄ = 7 ;  НОД (203 , 221) =1

x₅ = 78 ;  НОД (71,221) = 1

X₆ = 91. При х₆ маємо НОД (х₆ – х₅, N) = НОД (91 – 78, 221) = НОД (13, 221) = 13

Таким чином один із співмножників  модуля N є 13, наприклад P=13. Тоді Q = N/P = 221/13 = 17. Перевіряємо правильність розв’язку, знайшовши P*Q = 221.

Задача 2

Факторизувати число N = 209, якщо x_i = x² + 1(mod N)                                        (11),

 прийнявши, що .

Розв’язок задачі:

x₁ = (17² + 1)mod 209 = 81

x₂ = (81² + 1)mod 209 = 83

НОД (2, 209) = 1 розв’язку немає.

x₃ = (83² + 1)mod 209 = 202

x₄ = (202² + 1)mod 209 = 50

x₃ - x₄ = |202-50| = 152.

НОД (152, 209) = 19.

Таким чином один із співмножників, наприклад P=19, тоді Q = 209/19 = 11.

Задача 3

Розв’язати порівняння 15^x º 9(mod 23) методом -Поларда.

Нехай с = 6.

Розв’язок задачі

Використовуючи (9) та (10), розрахунки зведемо в таблицю. Знайдемо

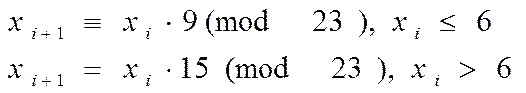
Використовуючи (5) та (7) розрахунки зведемо в таблицю.

Цикл	Довжина	xi	u	V	xi	t	v
1	2	x0 = 9	0	1	X1 = 20	1	1
		X1 = 20	1	1	X2 = 1	2	1
		X2 = 1	2	1	X3 = 1	2	2
		X3 = 9	2	2	X4 = 20	3	2
					X5 = 1	4	2
					X6 = 9	4	3

Таким чином при u=2,v=2, і u=4,v=3 отримуємо одне і теж значення x_i – x₆ = x₃ = 9.

Підставивши значення в (v = 2, w = 3, t = 4, u = 2) отримаємо

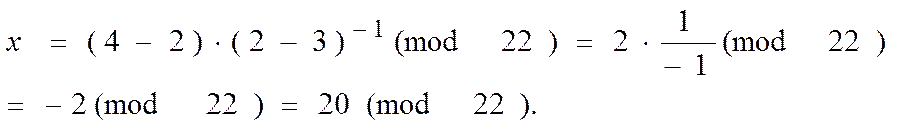
Задача 4

Розв’язати рівняня методом -Поларда 20 º7^x (mod 23).

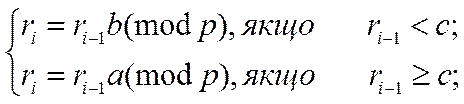
c = 10, r₀ = b = 20, a = 7.

Розв’язок задачі:

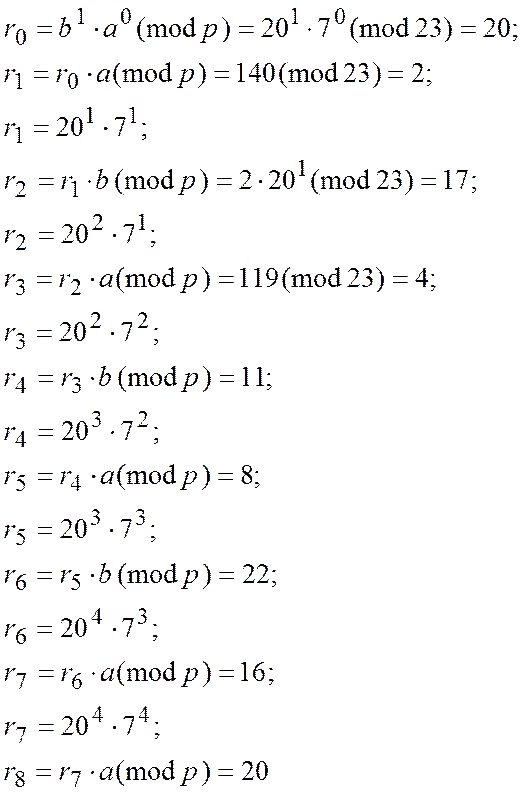
Таким чином r₈ = r₀, причому r₈ можна представити як

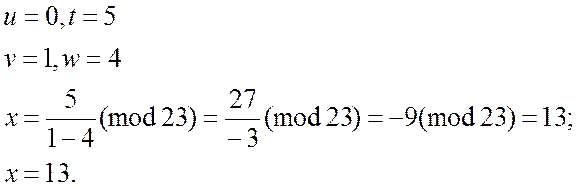
7.4 Задачi для самостiйного розв'язку.

1.Розв'яжіть порівняння 15 º 4 (mod 23) методом  - Поларда.  Перевірте правильність розв'язку порівняння.

4= (k+2)mod 25, де k-номер по журналу, k ¹ 3

2.Факторизуйте модуль  RSA перетворення методом  - Поларда, якщо

№	1	2	3	4	5	6	7	8	9	10	11
N	391	221	299	209	247	133	217	253	161	91	437

i = k (mod 12), k - номер по журналу.

7.5 Контрольнi запитання.

1. Сутність метода Поларда?

2. Чому метод Поларда називають -методом?

3.Яка ознака того, що рiшення знайдено?

4.Що таке "факторизацiя модуля"?

5. Які вимоги до модуля N?

6. Як розраховується значення функції Ейлера для RSA перетворення?

7. Дайте оцінку складності RSA криптоаналізу методом  Поларда?

8. Які прості числа називаються “сильними”?

9. В чому полягає криптоаналіз дискретних логарифмів методом -Поларда?

10. Як обирають коефіцієнти с при розв’язку дискретного логарифмічного порівняння.

11. Як знайти НОД двох чисел

12. Які обмеження притаманні методу  Поларда при факторизації та розв’язку дискретних логарифмічних порівнянь.

Практичне заняття №8

Криптоаналiз RSA методом двiйкового решета.

8.1. Мета заняття: вивчити метод двiйкового решета для криптоаналізу RSA [1, 13].

8.2Основнi відомості iз теорії.

Криптоаналіз RSA методом двійкового решета.

Метод грунтується на тому, що шукаються такі числа x и y, щоб виконувалося порівняння: 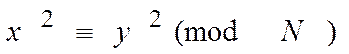                                      (1)

Порівняння можна представити як:

,

або використавши формулу різниці квадратів маємо:

                                                          (2)

Проаналізувавши даний вираз, маємо, що він виконується, якщо значення зліва порівнюється з N.

                                                                          (3)

Умова буде виконуватися, якщо :

1)  або                                                     (4)

2)  або                                                                     (5)