Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 21

3) або                                                                                  (6)

Якщо ми знайдемо такі x і y, які задовольняють (5) або (6), то

НСД (x-y,N) або НСД(x+y,N) дасть один з співмножників числа N.

Метод факторизації з використанням двійкового решета заключається в тому, що у якості деяких допоміжніх параметрів обирають числа Z, такі, що

Далі розглядають ряд

Решето організується за допомогою знаходження деякої бази в полі , де -добуток простих чисел, , і

Далі розкладається по базі . Потім знаходять числа x та y, які задовольняють вираз (1).

8.3. Приклади розв'язку задач

Задача 1

Факторизувати модуль N, використовуючи метод двійкового решета, якщо N = 377.

Розв’язок задачі:

Знаходимо

                                                                                                                       Таблиця 1

x	Z = x+	Z 2  mod N	2	3	5	7	Залишок
1	20	23	-	-	-	-	23
2	21	64	6	-	-	-
3	22	107	-	-	-	-
4	23	152	3	-	-	-	19
5	24	199	-	-	-	-	199
6	25	248	3	-	-	-	31
7	26	299	-	-	-	-	299
8	27	352	5	-	-	-	11
9	28	30	1	1	1	-
10	29	87	-	1	-	-	29
11	30	146	1	-	-	-	73
12	31	207	-	2	-	-	23
13	32	270	1	3	1	-
14	33	335	-	-	1	-	67
15	34	25	-	-	2	-

У першому стовпчику задаємо значення x, у другому х+19, у третьому Z ²  mod N. Далі значення Z ²  mod N розкладається на співмножники бази Р¢, точніше робиться спроба, - це числа 2, 3, 5, 7, добуток цих чисел р¢ = 210. Із таблиці бачимо, що число 23 не розкладається на співмножники бази. Число 64 розкладається на співмножники – 2 (2⁶ = 64).

Якщо Z ²  mod N повністю розкладається на співмножник або співмножники р¢, то таку спробу вважаємо позитивною та помічаємо рядок знаком “+”. Для успішної факторизації необхідно не менше k, k – де – число співмножників бази розкладу, позитивних експериментів. Потім, перемножуючи значення стовпців Z ²  mod N  та результати розкладу по базі, необхідно скласти порівняння виду

.

Наприклад, другий рядок (тільки одна) дає такий результат

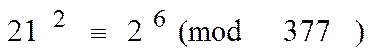
або

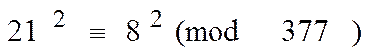
Тоді x = 21, y = 8; x-y = 21-8 = 13.

Далі НCД (x-y, N) = НCД (13, 377) = 29

Тому, наприклад P = 13, Q = 29 і N = 13*29 = 377.

Аналогічно можна взяти 15 рядок. Тоді маємо

.

Задача №2.

Нехай відомо, що в RSA cистемі використовується відкритий ключ D_k = 107, а модуль перетворення N = 209. Необхідно знайти особистий (секретний) ключ E_k та оцінити складність криптоаналізу.

Розв’язок задачі.

Здійснимо в декілька етапів. На першому факторизуємо модуль N, використовуючи метод двійкового решета. Потім, розв’язавши ключове порівняння, знайдемо особистий ключ D_k. В завершення оцінимо складність криптоаналізу, основний етап якого складає факторизація.

Розрахунки зведемо в таблицю 2, при цьому НСД будемо знаходити, використовуючи алгоритм Евкліда. Сутність алгоритма Евкліда:

Нехай

a₁ = x-y; a₂ = N

1)  if a₁ =a₂ then НСД:= a₂,

2)  a₁ := max(a₁, a₂)

a₂ := min(a₁, a₂)

3)a₁/a₂ ®a₃ =r

4) if a₃ = 0 then НСД :=a₂, END

5) a₁:= a₂; a₁:= a₃; goto 3).