Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 7

Рішення цього рівняння можна отримати з допомогою ланцюгових дробів:

                                                            (2.6)

                                            (2.7).

Відношення а/b розкладається в ланцюговий дріб.  - порядок  ланцюгового дробу, тобто коефіцієнт, у якого залишок рівний нулю.

Знаходимо параметри:

а/b  представляється у вигляді ланцюгового дробу.

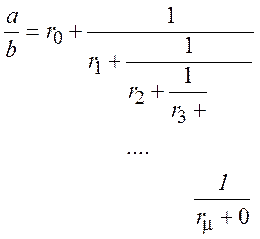                                                       (2.8)

μ - порядок ланцюгового дробу, перший коефіцієнт, у якого залишок рівний 0

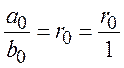
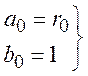                                                                           (2.9)

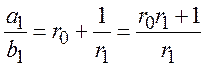
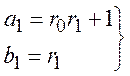                                                      (2.10)

для всіх членів, що залишилися,  починаючи з третього, справедливо:

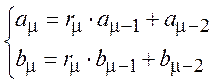                                                               (2.11)

При великих N – велике значення μ.  μ ≈ ⅓ N. Таким чином, для розв’язку порівняння (2.5). Необхідно представити а/b в вигляді ланцюгового дробу, визначивши при цьому значення r₀, r₁, …r_m та значення m. Потім визначитися згідно (2.9) –(2.11) a, m, b та x і y.

2.3 Приклади розв’язку задач

Задача 1

Нехай Р=11, Q=7, Е=37. Побудуйте ключову пару (E_k, D_k) для RSA-перетворення.

Розв’язок задачі:

Модуль перетворення має значення

N = P*Q = 11*7 = 77

Розраховуємо значення функцій Ойлера

j(N) = (P-1)(Q-1) = 10*6 =60 = 2³ 3*5

Для знаходження D_k ключа розв’яжемо порівняння

Представимо це порівняння у вигляді (2.4)

Підставимо значення j (N_j) та E_k маємо

представимо а/b у вигляді ланцюгового дробу

 

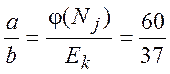
60/37=1+23/37; 37/23=1+14/23; 23/14=1+9/14; 14/9=1+5/9; 9/5=1+4/5; 5/4=1+1/4; 4/1=4+0;

Значить           =6;

Тоді значення можна знайти з виразу

;

Підрахуємо коефіцієнти, а₀, а₁, а₂, а₃, а₄ та а₅.

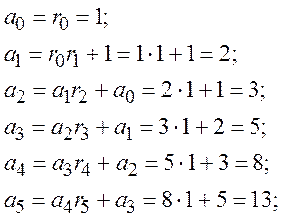
Визначимо ключ розшифрування

 y = D_k = (-1)⁶*13 = 13

Перевірку здійснюємо підстановкою значень E_k та D_k в основне порівняння.

.

Таким чином (E_k =37 та D_k= 13) є ключова пара RSA-перетворення.

Задача 2

Нехай Р=11 і Q=7. Побудувати пару (E_k, D_k) для RSA-перетворення, обґрунтувавши та вибравши один із випадкових ключів.

Розв’язок задачі:

Знаходимо модуль перетворення та значення функції Ойлера j (N)

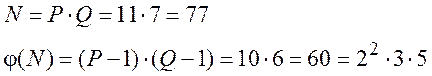
Порівняння виду

Залишимо у вигляді Діафантового рівняння

.

Вибравши випадково E_k ключ взаємопростий з функцією Ейлера, тобто (E_k, j (N)) = 1 маємо

.

Тепер представимо a/b у вигляді ланцюгового дробу.

 

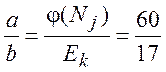
60/17=3+9/17; 17/9=1+8/9; 9/8=1+1/8; 8/1=8+0;

Таким чином

    =3.

Розраховуємо значення y=D, використовуючи співвідношення (2.6)

;

Знаходимо рекурентне значення а₂.

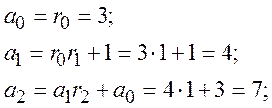
Підставивши значення в а₂. (2.6) маємо

Таким чином пара

складає RSA ключову пару.

Перевірка:

Підставивши значення ключів E_k =17та D_k = 53 маємо

.

Задача 3

Нехай Р=11 і Q=7. Виберемо Е=9 в якості випадкового ключа і побудуємо пару (E_k, D_k) для RSA ключів.

Розв’язок задачі:

Знаходимо модуль RSA  перетворення та значення функції Ейлера.

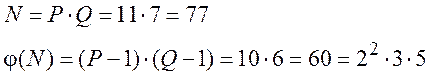
Ключ D_k знайдемо із порівняння (2.6)

Далі зведемо вищенаведене порівняння до Діафантового рівняння

 

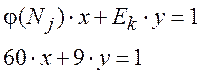
Знайдемо розклад ланцюгового дробу.

 

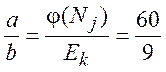
60/9=6+6/9; 9/6=1+3/6; 6/3=2+0;

Оскільки НЗД, то рішення для пари ключів (E_k, D_k) немає.

2.4 Задачі для самостійного розв’язку

1.Побудувати пару (E_k , D_k) для криптоаналізу RSA, якщо  (значення Р і Q дивись у таблиці )

n	1	2	3	4	5	6	7	8	9	10
Pп	29	11	11	11	23	7	29	17	19	19
Qп	11	17	23	13	17	23	7	7	7	11

  де

       - номер за списком

Якщо , то .

2.Розв’язати порівняння, якщоN = N_п  (значення Р і Q дивись у таблиці )

n	1	2	3	4	5	6	7	8	9	10
Nп	187	203	297	189	351	209	133	391	143	145