Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 8

  де

       - номер за списком

Якщо , то .

2.5 Контрольні запитання:

1.  Дати визначення несиметричних шифрів.

2.  Оцінка стійкості та стійкості RSA криптосистем

Практичне заняття №3

3.  Криптографічні перетворення в групах точок еліптичних кривих.

3.1. Мета

Вивчити методи виконання операцій складання і подвоєння в групах точок еліптичної кривої, що виконуються при визначенні відкритого ключа [1, 6, 14, 15]

3.2 Теоретичні відомості

Складність перетворень в групах точок еліптичної кривої пропорційно ,  - порядок базової точки на еліптичній кривій, k – коефіцієнти. Ця складність набагато більше, ніж субекспоненціальна , яка забезпечується в полях і кільцях.

Для підвищення складності системи необхідно збільшувати розміри параметрів, наприклад n, однак це само по собі підвищує складність криптографічних перетворень.

У сучасній криптографії знаходять застосування еліптичні криві.

Еліптичні криві над  простим полем

Нехай задано еліптичну криву над полем GF(q),

q=P, P-просте.

                                             (3.1),

де у і х – точки еліптичної кривої;

а і b- параметри еліптичної кривої, котрі вибираються над полем Р;

 а і b b повинні задовольняти умові

                                                         (3.2),

При представленнях застосовуються операції складання, подвоєння і скалярного множення.

подвоєння є частковим випадком, коли Р₁ = Р₂

 

Правило складання має вид:

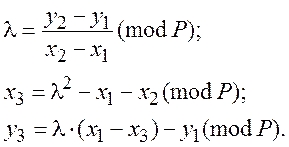                                                   (3.3)

Правило подвоєння має вид:

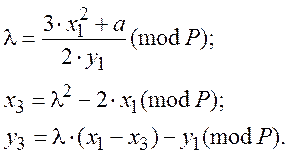                                                   (3.4)

Операція скалярного множення в групах точок еліптичної кривої еквівалентна операції піднесення до ступеня в полі GF(Р) та має вид:

Q = d*G(mod P)                                                            (3.5)

де d –число, 1£ d£ n-1;

G – базова точка на еліптичній кривій;

n – порядок базової точки.

Число d - особистий (секретний) ключ, а G - базова точка еліптичної кривої з координатами (x_g, y_g). Вираз (3.5) можна представити як

Q = G+G+… +G, де G+G+… +G = d                                                  (3.6),

Тобто у виді суми із d базових точок.

Еліптичні криві над розширеним полем G(2^m).

У цьому випадку застосовуються криві вигляду:

,                                                (3.7)

де

х і у – координати точок на еліптичній кривій;

a і b- параметри еліптичної кривої, поліноми m-ой міри ;

f(х) – примітивний поліном над полем GF(2^m) .

Поліном називається примітивним, якщо він не приводиться і породжує поле порядку  .

Точки  також є поліномами не вище m-ої міри.

Складання виконується за правилом

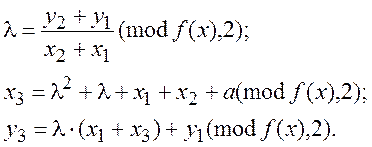                                                 (3.8)

f(x)- примітивний поліном, еквівалентний примітивному елементу.

Подвоєння виконується за правилом

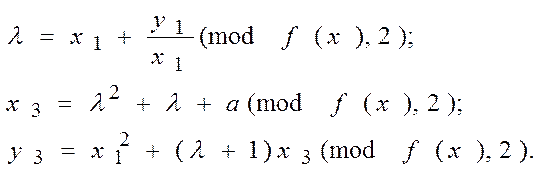                                                                   (3.9)

3.3 Приклади розв’язку задач

Приклад 1.

Скласти точки P1 і P2.  P1=(12, 19), P2=(5, 4). Якщо еліптична крива має вид

, тобто a = 1, b = 1, P = 23.

Розв’язок задачі:

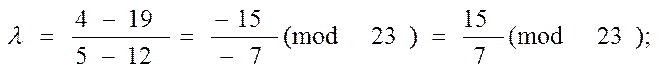
Знаходимо в полі G(23) обернений елемент Z, розв’язавши порівняння

7*Zº1 (mod 23).

Це порівняння має розв’язок при Z = 10, тому

l = 15*10 (mod 23) = 12

= 12² – 12 –5 = 144 - 12 – 5 (mod23) = 127 mod23 = 12 mod23

=12*(12 - 12) - 19(mod23) = 4mod23

Таким чином

P₁ + P₂ = (x₁, y₁) + (x₂, y₂) = P₃ = (x₃, y₃) = (12, 4)

P3=(12,4)

Приклад 2.

Знайти точку рівну 3*P1.  P1=(6,17);

Еліптична крива має вид

, тобто a=1,b=1;

Розв’язок задачі:

Спочатку подвоїмо точку Р₁

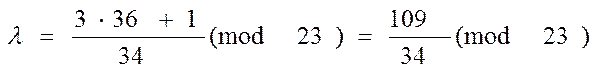
Знайдемо елемент, зворотний 34

34*Z º 1(mod 23) º 11*Z º 1(mod 23); Z=21.

l = (109*21)mod 23

Далі x3= 144 - 2*6 mod23=132 mod23=17 mod23

y3= 12(6-17) – 17 mod23= -149 mod23 = 12 mod23

Таким чином 2*P₁ = 2*(6, 17) = (17, 12)

Тепер складемо її з початковою точкою, тобто

P₁ + 2P₁ = (6, 17)+(17, 12) = P₃ = (x₃, y₃)

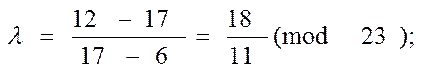
Далі знаходимо x₃ та y₃. Розв’язавши порівняння

11*Z º 1(mod 23)

Z=21 і l = 18*2 (mod 23) = 10

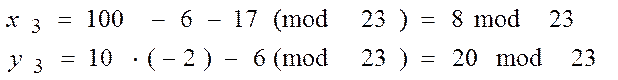
У результаті отримали точку (8,20), тобто