|
|
M2 |
|
Mn-1 |
Mn |
||||
|
|
|
||||||||
|
Ka |
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|||||||||
|
|
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|||||||
С1 |
С2 |
С3 |
Сn-1 |
Cn=Imn |
Рис. 5.1.
Оскільки довжина імітоприкладки дорівнює lімп=128 біт, то згідно (6) граничне значення ймовірності обману можна оцінити як:
![]()
Необхідно відмітити, що одночасно з формуванням імітоприкладки здійснено зашифрування повідомлення М. При цьому довжина зашифрованого повідомлення дорівнює довжині вихідного повідомлення, тобто автентифікацію здійснено без збільшення довжини зашифрованого повідомлення. Особливістю цього режиму є те, що додатково використовується ключ автентифікації. Якщо повідомлення не повинне зашифровуватись, то в цьому випадку до нього додається імітоприкладка і довжина автентифікованого повідомлення збільшується на lб=128 бітів, а саме автентифіковане повідомлення має вид {M, Іімп}. Основною перевагою такого методу автентифікації є висока швидкість перетворення і, як наслідок, можливість обчислення значення імітоприкладки в реальному плині часу. Основним недоліком є те, що використовувані ключі Кз та Ка є симетричними, а тому не дозволяють реалізувати захист на основі моделі взаємної недовіри.
Приклад 3. Задача “парадокс” днів народження. Ця задача може бути сформульована таким чином. Чому дорівнює мінімальне значення k, при якому ймовірність того, що, у крайній мірі, у двох осіб із групи в k осіб дні народження співпадуть, буде Рз.
Розв’язок задачі здійснити без урахування 29 лютого при умові, що кожен день народження рівно ймовірний.
Розв’язок
задачі. Введемо ймовірність ![]() та знайдемо
ймовірність того, що в групі із k осіб дні народження не співпадуть,
позначивши її як
та знайдемо
ймовірність того, що в групі із k осіб дні народження не співпадуть,
позначивши її як ![]() . Зрозуміло, що:
. Зрозуміло, що:
![]() ,
,
тому
![]()
Зрозуміло
також, що k![]() 365.
365.
Знайдемо число різних способів N, якими можна одержати k значень без повторень. Для першого елементу ми маємо 365 значень без повторень, для другого 364, які залишились, і так далі. Тому загальне число підходящих способів
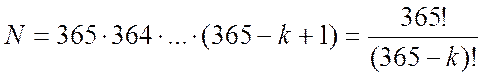
Якщо виключити умову відсутності спів падань днів народження, то кожен елемент (подія) може набувати любого із 365 можливих значень. Тому загальна сума можливих подій дорівнює 365k. Тому ймовірність відсутності спів падань дорівнює відношенню числа варіантів без співпадань до загального числа варіантів.
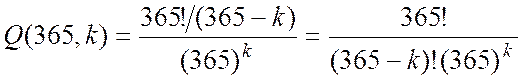 (13)
(13)
Тому
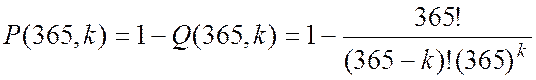
В таблиці 5.1 наведені наближені значення P(365,k)
Значення P(365,k)
k |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
P |
0,13 |
0,4 |
0,71 |
0,89 |
0,97 |
0,99 |
0,999 |
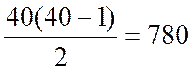 різних пар,
різних пар,
тому й імовірність для k=40 в таблиці достатньо велика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.