Информатика и выч. техника \ Основы теории защиты информации

Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 11

Тест Поккера

Нехай m є додатнє ціле число, таке що

Розділимо послідовність Y на k не перекриваючих частин, кожна довжиною m, нехай i буде число з'явлення послідовності i довжиною m i – того біту. Тест Поккера дозволяє визначити, чи дійсно послідовності довжиною m кожна приблизно з'являються стільки ж разів, скільки чекається у випадковій послідовності. Параметр:

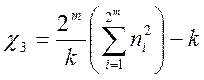
підчиняється розподілу з ступенями свободи.

Відмітимо, що тест Поккера є узагальненням частотного методу – при тест Поккера співпадає з частотним.

Тест серій

Тест серій дозволяє визначити, чи дійсно число нулів або одиниць (серії) різної довжини в послідовності Y такі ж як і у випадковій послідовності. Бажане число інтервалів довжиною і у випадковій послідовності n є

Нехай k буде рівним найбільшому цілому числу і, для якого . Нехай також B та G буде числом блоків і інтервалів відповідно довжиною і в Y для кожного і, . Тоді параметр

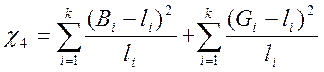
підчиняється розподілу з ступенями свободи.

Автокореляційний тест

Метою автокореляційного тесту є перевірка ступеню зв'язку між і її зсувами. Нехай d фіксоване ціле число, . Число бітів у Y послідовності дорівнюється

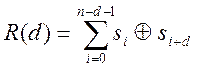Статистика параметру .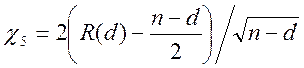

Приблизно підчиняється нормальному розподілу, якщо . Авто кореляційний метод повинен бути двостороннім, щоб розглядати його як для малих значень , так і для великих.

4.3. ПРИКЛАДИ РОЗВ'ЯЗАННЯ ЗАДАЧ

Задача №1

Розглянемо послідовність Y довжиною n=160, яку сформуємо із чотирьох 40 бітових послідовностей Y₀.

Y₀=11100 01100 01000 10100 11101 11100 10010 01001

1) Частотний (монобітний тест)

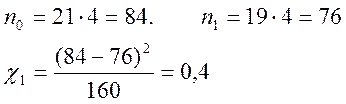
2) Двобітовий тест

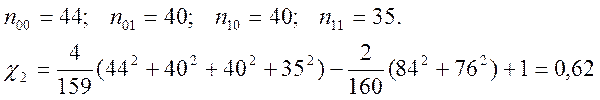
3) Тест Поккера

Нехай r=3 і k=53. Блоки 000, 001, 010, 011, 100, 101, 110, 111 з'являються відповідно 5, 10, 6, 4, 12, 3 біта 7 разів. Значення параметру

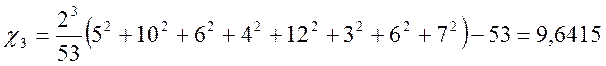4) Тест серій

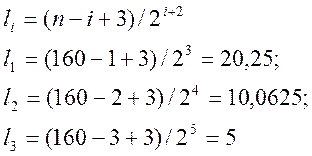
мається 25, 4 та 5 блоків довжиною 1, 2, 3 відповідно, 8, 20 та 12 інтервалів довжиною 1, 2 та 3 відповідно. Параметр приймає значення .

5) Автокореляційний тест

Якщо d=8, то R(8)=100.

Значення статистичного параметра

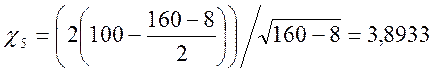Для рівня значимості порогові значення x₁, x₂, x₃, x₄ та x₅ дорівнюють 3.8415, 5.9915, 14.0671, 9.4877, 1.96 відповідно.

Бачимо, що послідовність проходить частотний (монобітний) тест, двобітовий тест та тест Поккера, але не проходить тест серій та автокореляційний тест.

4.4. ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РОЗВ'ЯЗКУ

4.4.1. Федеральним стандартом США FIPS – 140 – 1, 140 – 2 використовуються 4 статистичні тести на випадковість. Замість вибору користувачами потрібних рівнів значимості задаються реальні границі. При чому довжина бітової послідовності 20000 бітів.

Монобітний тест. Кількість n₀ та n₁, .

Тест Поккера. Статистичний параметр вираховується для m=4; тест виконується, якщо .

Тест серій. Тести проходять, якщо кожен із 12 номерів та , , знаходиться на границях відповідного інтервалу згідно таблиці:

Довжина серії	Відповідний інтервал
1	2267 – 2733
2	1079 – 1421
3	502 – 748
4	223 – 402
5	90 – 223
6	90 – 223

Тест довжин серій. Цей тест проходить, якщо не існує ніяких серій довжиною 34 або більше. Для високозахищених застосувань FIPS – 140 – 1 зобов'язує, щоб 4 тести виконувались при кожній ініціалізації генератора випадкових бітів.

4.4.2. Необхідно розробити слідуючі процедури на мові С++ або іншій мові.

а) генерація псевдовипадкової послідовності довільної довжини з використанням лінійного рекурентного регістру, закон генерації якої визначається відповідно до примітивних поліномів, наведених в таблиці: