Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 17

                                                          (3)

Відкритий ключ доступний усім користувачам системи.

2.На цьому етапі цифровий підпис формується у вигляді двох компонентів: .

Ці компоненти формуються на основі розв'язку класичного порівняння:

                                    (4)

де  - первісний елемент у полі, h=  - хеш–функція інформації М,  - відкритий ключ, Р – модуль перетворення.

Перша компонента ЦП r розраховується як

                                                 (5)

Підставимо (5) та (3) у (4), маємо:

або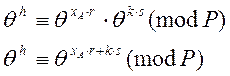                                          (6)

Порівняння (6) має розв’язок у вигляді:

                                                         (7)

(7) є фундаментальним співвідношенням, тому що дозволяє обчислити другу компоненту ЦП, а саме :

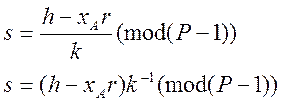                                       (8)

Перевірка здійснюється всіма користувачами, які володіють відкритим ключем та загальносистемними параметрами. Стійкість перетворення визначається складністю розв'язку порівняння (3) відносно знаходження особистого ключа  Х .

В якості ЦП на міжнародному рівні та в США знайшли поширення криптоалгоритми Х 9.30 (DSA) та Х 9.62 (ECDSA) [6, 15]. У таблиці 6.1 наведено відповідність між елементами та операціями групи F (DSA) та групи для Е (F).

Інформація про групи для DSA та ECDSA.

                                                                                                                              Таблиця 6.1

Група	F	Е (F)
Група елементів	Множина цілих чисел (1, 2,…, р – 1)	Точки (х, у), які задовольняють порівнянню еліптичної кривої та точка нескінченності О.
Операція в групі	Множення за модулем Р	Додавання точок
Позначення	Елементи F: g, h Множення: g  h (mod p) Ступінь g (mod p)	Елементи Е (F): R, G. Додавання R+G(mod f(x), p) Множення (скалярне): R G(mod f(x), p)
Сутність проблеми Дискретного Логарифма	При відомих Y, g та р  F знайти ціле d із порівняння Y = g (mod p)	При відомих G та QE(F), f(x) та р знайти ціле d із порівняння Q = d G (mod f(x), p)

У таблиці 6.2 наведено перелік загально системних параметрів та ключів DSA та ECDSA.

Параметри та ключі DSA та ECDSA.                                                Таблиця 6.2

DSA	ECDSA
1. p та q – прості числа, причому q /р – 1	1. Параметри еліптичної кривої a та b, параметри поля F(q), q = p, де р – просте, або q = p, та примітивний поліном m – го ступеня
2. q – елемент порядку q в полі F	2. G – точка порядку n в групі точок Е (F)
3. Група, яка використовується. g, g, g, ..., g(mod p) (mod q)	3. Група, яка використовується О, G, 2G, ..., (n - 1) G (mod f(x), p) або (mod p)

У таблиці 6.3 та 6.4 наведено в порівнянні алгоритми виробки та перевірки відповідно ЦП для DSA та ECDSA.

Виробка підпису для DSA та ECDSA.

                                                                                                               Таблица 6.3

DSA	ECDSA
1.  Сформувати випадкове ціле k  [1, q - 1].	1. Сформувати випадкове ціле k  [1, q - 1].
2. Обчислити r' = g (mod p)	2. Обчислити r' = k G (mod p)
3. Обчислити r – елемент підпису r = r' (mod q)	3. Обчислити r – елемент підпису r = х(mod n)
4. Обчислити хеш – функцію інформації М l = H(M).	4. Обчислити хеш – функцію інформації М l = H(M).
5. Обчислити s елемент цифрового підпису s = k (l + x r) mod q	5. s = k (l + d r) mod n
6. ЦП для М є пара цілих чисел r, s	6. ЦП для М є пара цілих чисел {r, s}

Перевірка ЦП DSA та ECDSA.