Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 22

Аналогічно, як і в задачі 1, для факторизації використовується двійкове решето.

При цьому

p = 2*3*5*7* = 210;

Значить N»P

Таблица 2

N/n	x	Z =ë  x+û	Z 2  mod N	2	3	5	7	Залишок
1	1	15	16	4	-	-	-	+
2	2	16	47	-	-	-	-	-47
3	3	17	80	4		1	-	+
4	4	18	115	-	-	1	-	-23
5	5	19	152	3	-	-	-	-19
6	6	20	191	-	-	-	-	-
7	7	21	23	-	-	-	-	-
8	8	22	66	1	1	-	-	-11
9	9	23	111	-	1	-	-	-37
10	10	24	158	1	-	-	-	-79
11	11	25	207	-	2	-	-	23-
12	12	26	47	-	-		2	+
13	13	27	102	1	1	-	-	17-
14	14	28	157	-	-	-	-	-
15	15	29	5	-	-	1	-	+
16	16	30	64	6	-	-	-	+
17	17	31	125	-	-	3	-	+
18	18	32	188	2	-	-	-	47

У таблиці 3 наведені позитивні рядки

Таблица 3

x	Z =ë x+û	Z 2  mod N	2	3	5	7	Залишок
1	15	16	4	-	-	-	+
3	17	80	4		1	-	+
12	26	47	-	-		2	+
15	29	5	-	-	1	-	+
16	30	64	6	-	-	-	+
17	31	125	-	-	3	-	+

Замінимо в таблиці всі парні числа 0, а непарні 1. У матриці розміром n x(n+1) із нулів та одиниць завжди можна обрати множину рядків, таку, що у всіх стовпцях буде парне число одиниць, а значить є сукупність рядків у яких

 Наприклад, розв’язок дають рядки {3,15}, {3, 17}, {15, 17}, {1}, {12}, {16}.

1.  15² º 2⁴(mod 209); 15² º 4²(mod 209)

x=15, y=4.

НСД(15-4, 209) = 11

P=11; Q=N:P=209:11=19

2.{3,15}

17² 29² º 5 ²4²(mod 209); (17*29)² º (20)²(mod 209)

x=75, y=20.

НСД(75-20, 209)

{15, 17}

29² º 5¹(mod 209)

31² º 5³(mod 209)

(3129)² º 5 ⁴(mod 209); (2931)² º 25 ²(mod 209);

x=63; y=25; (x-y, 209) НСД=(38, 209)=(219, 209) = 19

Використовуючи алгоритм Евкліда маємо

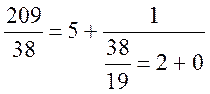
a₁ = 209; a₂ = 38

P=209:19=11;Q=19

209:38=5; r=19

a₁ = 38; a₂ = 19

39:19=2; r=0;

НСД (a₁, a₂)=a₂ = 19

Тепер розв’яжемо ключове порівняння

D_k = 103; N=209; j(N)= 10*18 = 180

j(N) (-k)+D_kE_k = 1;     180(-k)+103E_k = 1

180x+103y = 1  x=(-1)^m+1b_m-1;  y = (-1)^ma_m-1;

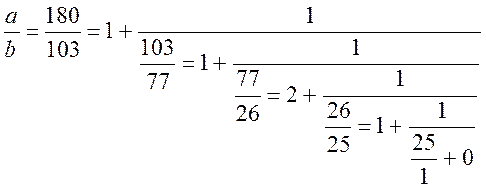
r₀ = 1;

r₁ = 1;

r₂ = 2;

r₃ = 1;

r₄ = 25;

m = 4;

a_m-1 = r_m-1a_m-2+a_m-3;             b_m-1 = r_m-1b_m-2+b_m-3;

a₃ = r₃a₂ + a₁;                b₃ = r₃b₂ + b₁

;

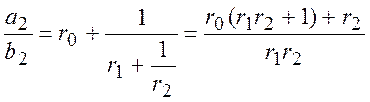a₂ = 1(1*2+1)+2 = 5; b₂ = 3

a₃ = 7

y = (-1)⁴7 = 7

Таким чином E_k = 7.

В таблиці 5 наведені значення складності криптаналізу, I₁ – методом Ленстри, І₂ – з використанням двійкового решета.

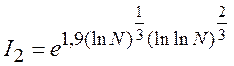
Таблиця 4