Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 18

DSA	ECDSA
1. Обчислити значення хеш – функції інформації М l = H(M).	1. Обчислити значення хеш – функції інформації М l = H(M).
2. Обчислити w = s (mod q).	2. Обчислити w = s (mod n).
3. Обчислити u = l w (mod q).	3. Обчислити u = l w (mod n).
4. Обчислити u = r w (mod q).	4. Обчислити u = r w (mod n).
5. Обчислити V` = q Y (mod p).	5. Обчислити V` = u G + u Q = (x, y1).
6. Обчислити V = V' (mod q).	6. Обчислити V = x(mod n).
7. Якщо V = r, то М цілісне та справжнє	7. Якщо V = r, то М цілісне та справжнє

Відповідно до сучасних поглядів, крипостійкість ЦП DSA та ECDSA визначається складністю розв'язання проблем дискретного логарифму (табл. 6.1). Складність криптоаналізу методом r- Поларда можна оцінити як 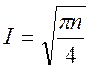 , де n – порядок базової точки на еліптичній кривій.

6.4. Приклади розв'язання задач:

Приклад 1. Оцініть імовірність обману, якщо для забезпечення цілісності та справжності використовується цифровий підпис DSA.

Розв'язок прикладу.

Спочатку зробимо оцінку, використовуючи границю Сімонсена

Р>, де  = 160 – довжина цифрового підпису, який використовується.

Р>2

Відомо також, що імовірність обману можна визначити як

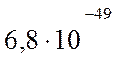
Р>,

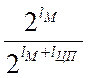де  - довжина інформації, яка підписується

а  - довжина цифрового підпису.

З цього співвідношення маємо

Р>.

Таким чином оцінка Сімонсена співпадає з останньою, одержаною через розмір множин повідомлень та автотентифікованих повідомлень за допомогою ЦП.

Приклад 2. Нехай ЦП здійснюється з використанням ECDSA, причому використовується крива .

В якості базової використовується точка  з порядком .

Необхідно:

– виробити особистий та відкритий ключі;

– виробити цифровий підпис згідно ECDSA, якщо ;

– перевірити цілісність та справжність повідомлення, у якого хеш-функція

Розв'язок прикладу.

Виробка ключів. Оскільки n=7, то ключем може бути будь-яке ціле .

Виберемо . Тоді відкритий ключ

.

тобто

.

Використовуючи афінний базис, спочатку визначаємо (13,7)+(13,7) = 2(13,7), тобто здійснимо подвоєння.

Якщо R₁ та R₂ є точки на еліптичній кривій відповідно з коефіцієнтами  та , то

,

причому

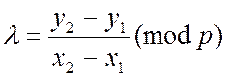
При подвоєнні , причому

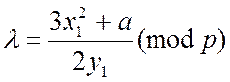
При подвоєнні точки (13,7) маємо (a=1)

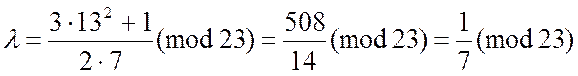
Знайдемо для 7 обернений елемент, розв'язавши порівняння

або еквівалентне цьому діафантове рівняння

.

Позначивши x = -k та y=z, маємо , a=23, b = 7.

Розв'язок шукаємо у вигляді

де  - є кількість членів ланцюгового дробу розкладу .

Представимо  у вигляді ланцюгового дробу

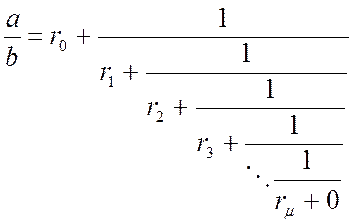
В результаті маємо

.

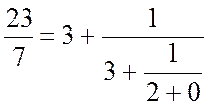Таким чином r₀ = 3, r₁ = 3, r₂ = 2, тоді

;

.

Дійсно, .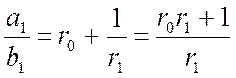

Тоді

.

Значить

.

.

Таким чином

.

Далі знайдемо

.

Використовуючи формули для складання точок, маємо

,

.

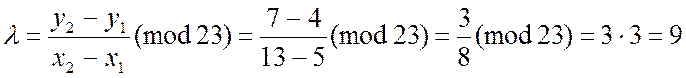Аналогічно x₃ дорівнює 17.

Таким чином, .

Результат:

особистий ключ d = 3;

відкритий ключ Q = (17, 3).

Виробку ЦП виконаємо згідно таблиці 6.3, в результаті маємо

1.  Виробимо .

2.  Обчислимо .

3.  Знаходимо x₁ = 17.

4.  Обчислимо перший компонент ЦП

.

5.  Обчислимо другий компонент ЦП

Таким чином

(r, s) = (3, 2).

Перевірку ЦП здійснимо відповідно до таблиці 6.4.

Нехай (r, s) = (3, 2).

1.  Відкритий ключ Q = (17, 3).

2.  Обчислимо .

3.  Обчислимо

.

4.  Обчислимо

;

.

5.  Знаходимо крапку

.

6.  Знайдемо .

7.  Обчислимо.

8.  Оскільки , то повідомлення цілісне та справжнє.

6.5 Приклади для самостійного розв'язання.

1. Оцініть імовірність обману, якщо для ЦП використовуються криптографічні алгоритми ГОСТ 34.310 – 95 або ГОСТр.34.10 – 2001.

2. Оцініть імовірність обману, якщо довжина ЦП , та 512 бітів.

3. Розв'яжіть приклад 2 при значенні  та 5.

4.Розв'язжіть приклад 2 в частині перевірки ЦП, якщо:

1) значення хеш – функції

2) значення вибрано довільним чином

3) значення вибрано довільним чином

4) значення  та вибрано довільно.

5. Розрахуйте складність криптоаналізу дискретного логарифму в групах точок еліптичної кривої, якщо

 та .

6. Знайдіть безпечний час криптосистеми ЦП в групах точок ЕК, якщо  та , а  та .